Bảy hằng đẳng thức đáng nhớ
Bảy hằng đẳng thức đáng nhớ là một phần kiến thức nền tảng trong chương trình Toán học cấp 2 và cấp 3, đặc biệt quan trọng trong đại số. Đây là những biểu thức toán học được rút gọn từ các phép biến đổi đồng nhất, giúp học sinh giải nhanh các bài toán khai triển, rút gọn biểu thức, phân tích đa thức thành nhân tử và giải phương trình.
Ý nghĩa và vai trò trong học tập
Việc ghi nhớ và vận dụng thành thạo các hằng đẳng thức giúp học sinh làm bài nhanh, chính xác hơn. Không chỉ dừng lại ở các bài tập trong chương trình học, các công thức này còn là công cụ hữu ích khi học giải tích, lượng giác hoặc tham gia các kỳ thi học sinh giỏi, thi tốt nghiệp, đại học.
Bảy hằng đẳng thức bao gồm
Bình phương của một tổng: (a + b)² =a² +2ab+b²
Bình phương của một hiệu: (a - b)² =a² - 2ab+b²
Hiệu hai bình phương: a² - b² =(a - b)(a + b)
Lập phương của một tổng: (a + b)³ =a³ +3a² b+3ab² +b³
Lập phương của một hiệu: (a - b)³ =a³ - 3a² b+3ab² - b³
Tổng lập phương: a³ +b³ =(a + b)(a² - ab + b² )
Hiệu lập phương: a³ - b³ =(a - b)(a² + ab + b² )
Lời khuyên
Học sinh nên học thuộc lòng kết hợp với thực hành thường xuyên để dễ ghi nhớ và ứng dụng linh hoạt trong nhiều dạng bài toán khác nhau.

Cách học hằng đẳng thứcBảy hằng đẳng thức là những công thức toán học quen thuộc, thể hiện mối quan hệ đồng nhất giữa các biểu thức đại số. Đây là kiến thức nền tảng trong chương trình toán học THCS và THPT, giúp học sinh rút gọn, khai triển biểu thức hoặc phân tích đa thức thành nhân tử một cách nhanh chóng và chính xác.
Những công thức này được gọi là “ đáng nhớ” vì tính ứng dụng rộng rãi và xuất hiện thường xuyên trong nhiều dạng bài toán, từ cơ bản đến nâng cao. Việc ghi nhớ và sử dụng thành thạo các công thức này giúp học sinh giải toán nhanh hơn, hạn chế sai sót và nâng cao tư duy logic.
Dưới đây là 7 hằng đẳng thức đáng nhớ:
(a + b)² =a² +2ab+b²
(a - b)² =a² - 2ab+b²
a² - b² =(a - b)(a + b)
(a + b)³ =a³ +3a² b+3ab² +b³
(a - b)³ =a³ - 3a² b+3ab² - b³
a³ +b³ =(a + b)(a² - ab + b² )
a³ - b³ =(a - b)(a² + ab + b² )
Tại sao nên học thuộc lòng?
Bảy hằng đẳng thức này là công cụ giúp giải toán hiệu quả, tiết kiệm thời gian trong các kỳ thi và khi giải các bài toán phức tạp ở bậc cao hơn. Khi làm bài toán đại số, nếu nhận diện được dạng hằng đẳng thức thì bạn có thể rút gọn hoặc biến đổi biểu thức rất nhanh, thay vì thực hiện các phép tính dài dòng.

Học sinh trong giờ ToánBài 1: Khai triển biểu thức
Áp dụng các hằng đẳng thức để khai triển các biểu thức sau:
a) (x + 3)²
b) (2a - 5b)²
c) (m - 4n)(m + 4n)
d) (x + y)³
e) (x - y)³
f) (3a + 2)³
g) (5x - 2y)³
Bài 2: Phân tích đa thức thành nhân tử
a) x² +6x+9
b) 4a² - 4ab+b²
c) 25x² - 49
d) a³ +b³
e) x³ - 8
f) 27a³ +64b³
g) 8x³ +27y³
Bài 3: Tính nhanh (nhẩm) bằng hằng đẳng thức
a) Tính 49²
b) Tính 102²
c) Tính 995²
d) Tính 1001³
e) Tính 98 × 102
Gợi ý:
Dùng (a ± b)² để tính bình phương gần số tròn chục.
Dùng a² - b² để tính tích hai số đối xứng quanh một trung bình.
Dùng (a ± b)³ khi cần tính lập phương gần số tròn.
Bài 4: Nhận diện hằng đẳng thức trong biểu thức phức tạp
a) Chứng minh: (x + y)² +(x - y)² =2(x² + y² )
b) Tìm x biết: (x - 2)² =9
c) Tìm x biết: x³ - 27=0
d) Phân tích biểu thức: x³ +3x² +3x+1
Bài 5: Luyện tập tổng hợp
a) Cho A=(2x - 3)² +4(2x - 3)+4
Tính A theo x.
b) Phân tích: x⁶ - y⁶ thành nhân tử
Gợi ý: Dùng hằng đẳng thức nhiều bước:
x⁶ - y⁶=(x³ )² - (y³ )² =(x³ - y³ )(x³ + y³ )
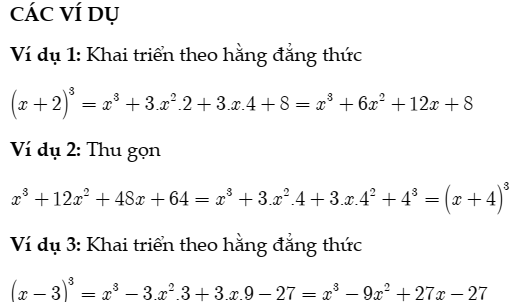
Một số ví dụ triển khai Dưới đây là một số bài tập vận dụng bảy hằng đẳng thức , từ cơ bản đến nâng cao, giúp bạn rèn luyện kỹ năng nhận diện và áp dụng các công thức một cách thành thạo.
Hiểu bản chất, đừng học vẹt
Trước khi học thuộc, hãy hiểu bản chất của từng hằng đẳng thức thông qua khai triển, minh họa bằng hình ảnh hoặc ví dụ cụ thể. Ví dụ:
(a + b)² =a² +2ab+b² → là diện tích hình vuông cạnh (a + b)
a² - b² =(a - b)(a + b) → chênh lệch bình phương là tích hiệu và tổng
Nhóm theo cặp để dễ nhớ
Hãy nhóm các công thức có cấu trúc tương tự để học:
Nhóm 1: Bình phương 2 số
(a + b)² =a² +2ab+b²
(a - b)² =a² - 2ab+b²
Nhóm 2: Hiệu bình phương
a² - b² =(a - b)(a + b)
Nhóm 3: Lập phương 2 số
(a + b)³ =a³ +3a² b+3ab² +b³
(a - b)³ =a³ - 3a² b+3ab² - b³
Nhóm 4: Tổng – Hiệu lập phương
a³ +b³ =(a + b)(a² - ab + b² )
a³ - b³ =(a - b)(a² + ab + b² )
Dùng mẹo ghi nhớ bằng chữ cái đầu hoặc vần điệu
Ví dụ học (a + b)³ :
" A cộng B mũ 3=A mũ 3+3 A bình B+3 A B bình+B mũ 3"
Dùng chữ cái đầu:
“ Bình cộng bình cộng 2 tích” → gợi nhớ (a + b)² =a² +2ab+b²
“ Lập cộng lập cộng 3 bình 1 tích” → gợi nhớ (a + b)³ =a³ +3a² b+3ab² +b³
Học qua bài tập thực tế
Làm thật nhiều bài tập ứng dụng mỗi hằng đẳng thức giúp bạn nhớ lâu hơn. Hãy làm bài tập theo từng nhóm công thức.
Dùng sơ đồ tư duy (mindmap)
Tự vẽ sơ đồ phân nhánh các công thức theo nhóm để hệ thống kiến thức, vừa trực quan, vừa giúp não ghi nhớ dễ hơn.
Làm thẻ học (flashcards)
Ghi công thức ở một mặt, ví dụ hoặc biểu thức cần phân tích ở mặt còn lại. Ôn đi ôn lại mỗi ngày 5– 10 phút, rất hiệu quả.