Cách chứng minh 3 điểm thẳng hàng
Trong hình học, việc chứng minh ba điểm thẳng hàng là một dạng bài kinh điển xuất hiện từ cấp THCS đến THPT. Đây không chỉ là kỹ năng cơ bản mà còn là điểm tựa cho rất nhiều bài toán lớn hơn như chứng minh ba đường thẳng đồng quy, chứng minh điểm nằm trên đường thẳng đặc biệt, hay xử lý bài toán tọa độ Oxy. Vì vậy, việc nắm chắc các phương pháp chứng minh ba điểm thẳng hàng sẽ giúp bạn làm bài nhanh hơn, chính xác hơn và tránh rối khi gặp bài khó. Bài viết dưới đây sẽ tổng hợp đầy đủ những cách chứng minh hiệu quả, kèm ví dụ minh họa rõ ràng.
Ba điểm được gọi là thẳng hàng khi chúng nằm trên cùng một đường thẳng. Nghĩa là nếu vẽ đường thẳng đi qua hai điểm bất kỳ trong ba điểm đó, điểm còn lại cũng phải nằm trên đường thẳng ấy.
Trong hình học phẳng, nhận biết và chứng minh ba điểm thẳng hàng giúp rút gọn cấu trúc hình vẽ và tìm ra mối quan hệ giữa các đoạn thẳng, góc hoặc tỉ số. Còn trong hình học tọa độ, kiểm tra ba điểm có thẳng hàng không giúp xác định nhanh phương trình đường thẳng hoặc nhận biết bài toán có lời giải hay không.
Ý nghĩa thực tế của việc chứng minh ba điểm thẳng hàng còn thể hiện trong các bài toán liên quan đến quỹ tích, tính khoảng cách từ điểm đến đường thẳng, hoặc phân tích hình phức tạp thành các phần đơn giản hơn.
Có nhiều phương pháp để chứng minh ba điểm thẳng hàng và mỗi phương pháp lại phù hợp với một dạng bài khác nhau. Có bài dễ dàng xử lý bằng vectơ, nhưng có bài lại nên dùng diện tích hoặc tỉ số để tránh tính toán dài dòng. Việc chọn phương pháp phù hợp sẽ quyết định tốc độ và độ chính xác của bài làm.
Nhìn chung, các phương pháp được dùng nhiều nhất gồm: dùng vectơ, dùng diện tích tam giác, dùng tỉ số đoạn thẳng, dùng phương trình đường thẳng, dùng góc hoặc dựa vào các định lý hình học đặc biệt. Điều quan trọng nhất là phải hiểu bản chất của từng phương pháp chứ không phải học thuộc công thức.
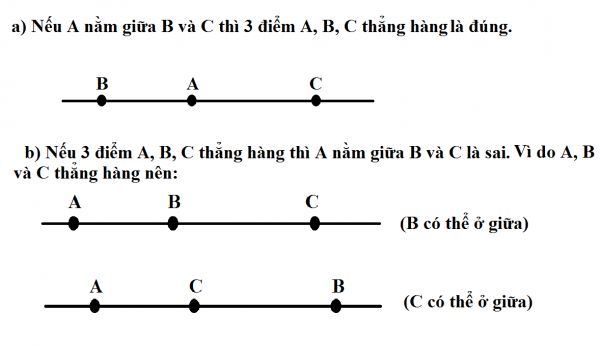 Đặc điểm của 3 điểm thẳng hàng
Đặc điểm của 3 điểm thẳng hàngCách chứng minh 3 điểm thẳng hàng bằng vectơ
Dùng vectơ là phương pháp mạnh và phổ biến nhất trong hình học hiện đại. Nguyên tắc rất đơn giản: ba điểm A, B, C thẳng hàng khi và chỉ khi hai vectơ AB và AC cùng phương. Hai vectơ được coi là cùng phương nếu tồn tại một số k sao cho AB=k· AC.
Để triển khai, bạn chỉ cần xác định hai vectơ AB và AC, sau đó so sánh từng cặp tọa độ. Nếu tỉ lệ giữa các hoành độ, tung độ (và cả z trong không gian) đều bằng nhau thì ba điểm chắc chắn thẳng hàng.
Ví dụ đơn giản: Cho A(1, 2), B(3, 6), C(5, 10). Khi tính vectơ AB=(2, 4), AC=(4, 8), ta thấy AC=2AB, vậy A, B, C thẳng hàng.
Phương pháp này cực nhanh trong bài toán tọa độ, đặc biệt khi bạn không muốn viết phương trình đường thẳng dài dòng.
Cách chứng minh 3 điểm thẳng hàng bằng diện tích tam giác
Một tam giác có diện tích bằng 0 thì ba điểm cấu tạo nên tam giác đó nằm trên cùng một đường thẳng. Đây là nguyên lý rất quan trọng mà học sinh hay bỏ qua.
Công thức diện tích tam giác ABC trong tọa độ Oxy là:
S=1/2 | xA(yB − yC)+xB(yC − yA)+xC(yA − yB) |
Nếu tính ra kết quả bằng 0, ba điểm thẳng hàng.
Ưu điểm của phương pháp này là tính trực tiếp, ít phải suy luận, phù hợp khi đề bài cho tọa độ lớn hoặc giá trị không đẹp. Tuy nhiên, nhược điểm là đôi khi tính toán hơi dài, nhất là khi các điểm có số lẻ hoặc phân số.
Ví dụ: Với A(1, 1), B(2, 2), C(3, 3), thay vào công thức sẽ được diện tích bằng 0, vậy ba điểm thẳng hàng.
Cách chứng minh 3 điểm thẳng hàng bằng hệ thức tỉ số
Nếu điểm B nằm giữa A và C thì ba điểm thẳng hàng và khi đó tỉ số AB/AC phải thỏa mãn một hệ thức nhất định. Ngược lại, nếu chứng minh được tỉ số đoạn thẳng trong bài liên quan đến một đường thẳng duy nhất, ta có thể suy ra ba điểm thẳng hàng.
Phương pháp này đặc biệt hiệu quả trong bài hình học phẳng, nơi có các định lý như Thales, Menelaus hoặc đường trung tuyến. Đặc biệt, khi tổng hợp hình với nhiều đường cắt nhau, chứng minh ba điểm thẳng hàng bằng tỉ số giúp rút gọn bài toán.
Ví dụ quen thuộc: Trong tam giác ABC, nếu M là trung điểm BC thì AM là đường trung tuyến. Trên AM có thể xuất hiện điểm D nào đó có tỉ số AD/A M cố định, từ đó suy ra D, A, M thẳng hàng.
Điều cần lưu ý khi dùng tỉ số là bạn phải chỉ ra được các đoạn thẳng liên quan nằm trên cùng một cấu trúc hình học để kết luận chính xác.
Cách chứng minh 3 điểm thẳng hàng bằng phương trình đường thẳng
Trong hệ tọa độ, đây là cách làm truyền thống và dễ hiểu với những bạn thích làm bài theo hướng đại số.
Bạn chỉ cần lập phương trình đường thẳng đi qua hai điểm, ví dụ d qua A và B, sau đó kiểm tra điểm C có thỏa mãn phương trình đường thẳng đó hay không.
Các dạng phương trình có thể dùng:
Phương trình qua hai điểm
Phương trình tổng quát ax+by+c=0
Phương trình tham số
Ví dụ: Viết phương trình đường thẳng AB rồi thay tọa độ điểm C vào. Nếu giá trị thỏa mãn, ba điểm thẳng hàng.
Ưu điểm của phương pháp này là dễ kiểm tra và ít phải suy luận hình học. Nhược điểm là với số liệu phức tạp, việc lập phương trình có thể hơi dài.
Cách chứng minh 3 điểm thẳng hàng bằng góc
Phương pháp góc thường dùng trong hình học phẳng cơ bản. Nếu hai góc kề nhau có tổng bằng 180 độ hoặc một góc tạo thành đường thẳng chứa hai điểm còn lại, ta có thể suy ra ba điểm thẳng hàng.
Trường hợp thường gặp là chứng minh điểm nằm trên đường cao, đường phân giác, tiếp tuyến hoặc trung trực. Khi đó, dùng góc sẽ nhanh hơn nhiều so với dùng tỉ số hoặc vectơ.
Ví dụ: Nếu trong tam giác ABC có điểm D sao cho góc ADC=180 độ, rõ ràng A, D, C thẳng hàng.
Ưu điểm của cách này là trực quan, dễ nhận biết trên hình. Tuy nhiên, không dùng được cho bài toán tọa độ.
 Sử dụng định lý về khoảng cách
Sử dụng định lý về khoảng cáchĐể hiểu rõ hơn, bạn có thể luyện 5 dạng bài thường gặp sau:
Dạng ba điểm cho tọa độ và yêu cầu chứng minh thẳng hàng bằng vectơ
Dạng cho tam giác và một điểm đặc biệt như trung điểm, chân đường cao, trung tuyến
Dạng liên quan đến đường thẳng cắt tam giác, có áp dụng Menelaus
Dạng bài trong không gian Oxyz
Dạng bài yêu cầu chứng minh hai điểm trùng nhau để suy ra thẳng hàng
Một ví dụ tiêu biểu:
Cho tam giác ABC, M là trung điểm AB, N là trung điểm AC. Chứng minh M, N và trọng tâm G thẳng hàng.
Ta biết trọng tâm G chia đoạn nối từ đỉnh tới trung điểm theo tỉ lệ 2:1. Từ đó dễ dàng suy ra M, N, G cùng nằm trên đường trung tuyến, nghĩa là thẳng hàng.
Bài toán nâng cao hơn:
Cho ba điểm A(1, 2, 3), B(3, 6, 9), C(-1, -2, -3). Hãy chứng minh ba điểm thẳng hàng.
Ta thấy vectơ AB=(2, 4, 6) và AC=(-2, -4, -6). Hai vectơ này cùng phương, chỉ khác dấu, vậy ba điểm thẳng hàng.
 Giờ học Toán trên lớp
Giờ học Toán trên lớpMẹo làm bài nhanh và tránh sai lầm
Một trong những mẹo quan trọng nhất là chuẩn bị hình vẽ rõ ràng trước khi bắt đầu cách chứng minh 3 điểm thẳng hàng, đặc biệt trong hình học phẳng. Hình rõ giúp bạn nhanh chóng nhận ra điểm nào có khả năng thẳng hàng và chọn phương pháp phù hợp.
Nếu làm bài tọa độ, hãy kiểm tra sự tương quan của các vectơ hoặc viết phương trình đường thẳng sao cho đơn giản nhất. Một mẹo hữu ích là luôn ưu tiên dùng vectơ trước khi dùng phương trình, bởi vectơ cho phép kiểm tra nhanh hơn.
Ngoài ra, cần tránh nhầm lẫn giữa tỉ số các đoạn thẳng không cùng phương hoặc áp dụng sai định lý Thales. Khi gặp bài nhiều điểm giao nhau, hãy tìm điểm trung gian giúp rút gọn bài toán.
Cuối cùng, khi trình bày bài thi, bạn nên lập luận ngắn gọn, rõ ràng, không bỏ thiếu bước và không viết quá dài. Điều này vừa giúp bạn tiết kiệm thời gian, vừa làm bài trở nên dễ theo dõi hơn.
Chứng minh ba điểm thẳng hàng là kỹ năng nền tảng trong hình học và xuất hiện xuyên suốt từ lớp 7 đến lớp 12. Việc nắm chắc các phương pháp như vectơ, diện tích tam giác, tỉ số đoạn thẳng, phương trình đường thẳng hay góc sẽ giúp bạn xử lý nhanh hầu hết các dạng bài từ cơ bản đến nâng cao.
Để thành thạo, bạn nên luyện mỗi dạng bài một vài lần và tìm cách rút gọn bước giải sao cho logic và tự nhiên nhất. Khi hiểu bản chất, bạn sẽ dễ dàng nhận ra phương pháp phù hợp ngay khi đọc đề, từ đó làm bài nhanh hơn và đạt điểm cao hơn.