Diện tích hình thang vuông
Hình thang vuông là một dạng đặc biệt của hình thang, được xác định khi một trong hai cạnh bên vuông góc với hai cạnh đáy. Nói cách khác, nếu trong một hình thang có ít nhất một góc bằng 90° , hình đó được gọi là hình thang vuông.
1. Đặc điểm nhận biết hình thang vuông:
Có hai cạnh đối song song (gọi là đáy lớn và đáy nhỏ).
Có một cạnh bên vuông góc với hai cạnh đáy, chính là dấu hiệu đặc trưng giúp phân biệt hình thang vuông với hình thang thường.
Cạnh vuông góc này cũng chính là chiều cao của hình thang vuông, giúp việc tính diện tích dễ dàng hơn so với các loại hình thang khác.
2. Mối quan hệ với các hình học khác:
Hình thang vuông có một phần tính chất của hình chữ nhật (vì có góc vuông).
Đồng thời, vẫn giữ đặc điểm của hình thang (có hai cạnh song song).
Do đó, có thể xem hình thang vuông như một bước trung gian giữa hình chữ nhật và hình thang thường.
3. Ví dụ minh họa:
Giả sử ta có hình thang ABCD, trong đó AB song song với CD, và cạnh AD vuông góc với AB và CD. Khi đó, hình thang ABCD được gọi là hình thang vuông tại A (và D).

Công thức
Nếu cạnh bên còn lại BC không vuông góc, ta vẫn có hình thang vuông, vì chỉ cần một cạnh bên vuông góc là đủ.
4. Ý nghĩa trong học tập và thực tế:
Hình thang vuông là một trong những hình học cơ bản được học ở bậc tiểu học và THCS. Nhờ đặc tính có chiều cao rõ ràng, hình thang vuông thường được dùng để làm ví dụ trong các bài học về diện tích, hoặc ứng dụng trong kỹ thuật và xây dựng khi cần đo đạc các phần diện tích có dạng nghiêng nhưng có một cạnh thẳng đứng.
Hình thang vuông là dạng đặc biệt của hình thang, có một cạnh bên vuông góc với hai đáy. Nhờ vậy, việc tính diện tích trở nên rất đơn giản chỉ cần biết độ dài hai đáy và chiều cao.
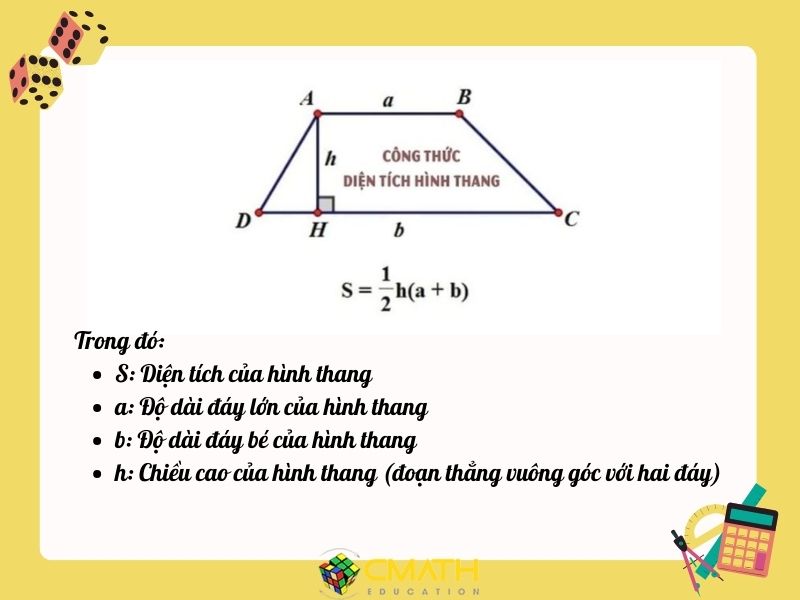
1. Công thức tổng quát:
Diện tích của hình thang vuông được tính theo công thức:
S=(a + b) × h / 2
Trong đó:
S là diện tích của hình thang vuông
a là độ dài đáy lớn
b là độ dài đáy nhỏ
h là chiều cao (cạnh vuông góc với hai đáy)
2. Giải thích công thức:
Công thức trên dựa vào quy tắc tính diện tích hình thang nói chung. Ta có thể coi hình thang vuông gồm một hình chữ nhật và một tam giác vuông ghép lại. Khi cộng diện tích hai phần này, ta thu được công thức trung bình cộng hai đáy nhân với chiều cao.
3. Ví dụ minh họa:
Cho hình thang vuông ABCD có:
Đáy lớn AB=10 cm
Đáy nhỏ CD=6 cm

Giải thích
Chiều cao AD=5 cm
Áp dụng công thức:
S=(10 + 6) × 5 / 2=16 × 5 / 2=40 cm²
Vậy diện tích của hình thang vuông ABCD là 40 cm² .
4. Một số trường hợp mở rộng:
Nếu không biết chiều cao mà biết cạnh bên nghiêng c và hiệu hai đáy, ta có thể tính:
h=√ (c² − (a − b)² )
Sau đó thay vào công thức S=(a + b) × h / 2 để tính diện tích.
5. Cách ghi nhớ nhanh:
“ Đáy lớn cộng đáy nhỏ, nhân chiều cao chia hai” – mẹo học đơn giản giúp học sinh dễ thuộc và ít nhầm khi làm bài.
Phần bài tập này giúp học sinh nắm vững công thức, rèn kỹ năng vận dụng và mở rộng khả năng tư duy qua các tình huống thực tế. Các bài được sắp xếp theo mức độ: từ cơ bản, có hướng dẫn, đến bài vận dụng thực tế gần gũi với chương trình học Toán tiểu học và THCS.
1. Bài tập cơ bản – áp dụng trực tiếp công thức:
Bài 1: Hình thang vuông ABCD có đáy lớn AB=12 cm, đáy nhỏ CD=8 cm và chiều cao AD=5 cm.
Tính diện tích của hình thang vuông ABCD.
Lời giải:
S=(a + b) × h / 2=(12 + 8) × 5 / 2=20 × 5 / 2=50 cm² .
→ Diện tích của hình thang vuông là 50 cm² .
Bài 2: Một hình thang vuông có đáy lớn 15 m, đáy nhỏ 9 m và chiều cao 4 m.
Tính diện tích của hình thang vuông đó.
Lời giải:
S=(a + b) × h / 2=(15 + 9) × 4 / 2=24 × 2=48 m² .
→ Diện tích của hình thang vuông là 48 m² .
Giải thích:
Đây là dạng bài xuất hiện nhiều trong chương trình Toán lớp 5 và lớp 6, giúp học sinh làm quen với cách thay số vào công thức và tính nhanh diện tích hình phẳng.
Giải thích công thức
2. Bài tập tìm ẩn – phát triển tư duy logic:
Bài 3: Hình thang vuông có đáy lớn 18 cm, đáy nhỏ 10 cm và diện tích là 56 cm² .
Tính chiều cao của hình thang vuông.
Lời giải:
S=(a + b) × h / 2
⇒ 56=(18 + 10) × h / 2
⇒ 56=28h / 2
⇒ 56=14h
⇒ h=4 cm.
→ Chiều cao của hình thang vuông là 4 cm.
Giải thích:
Dạng bài này thường gặp trong Toán lớp 6 – Chương “ Diện tích các hình phẳng” , yêu cầu học sinh biết biến đổi công thức và suy ra đại lượng còn thiếu.
3. Bài tập kết hợp định lý Pythagoras – dành cho học sinh khá giỏi:
Bài 4: Một hình thang vuông có đáy lớn 20 cm, đáy nhỏ 8 cm và cạnh bên nghiêng 13 cm.
Tính diện tích của hình thang vuông.
Lời giải:
Hiệu hai đáy: 20 − 8=12 cm.
Áp dụng định lý Pythagoras cho tam giác vuông, ta có:
h² +12² =13² ⇒ h² =169 − 144=25 ⇒ h=5 cm.
S=(a + b) × h / 2=(20 + 8) × 5 / 2=28 × 5 / 2=70 cm² .
→ Diện tích của hình thang vuông là 70 cm² .
Giải thích:
Bài này giúp học sinh luyện kết hợp kiến thức giữa hình học và đại số, thường gặp trong Toán lớp 7, phần luyện tập mở rộng.
4. Bài tập thực tế – gần gũi với chương trình học hiện nay:
Bài 5: Một mảnh đất có dạng hình thang vuông, đáy lớn dài 30 m, đáy nhỏ dài 20 m và cạnh bên vuông góc dài 10 m. Người chủ định trồng cỏ trên toàn bộ mảnh đất. Hỏi diện tích phần đất cần trồng cỏ là bao nhiêu mét vuông?
Lời giải:
S=(a + b) × h / 2=(30 + 20) × 10 / 2=50 × 5=250 m² .
Khi học và làm bài tập về diện tích của hình thang vuông, nhiều học sinh thường mắc phải một số lỗi cơ bản do nhầm lẫn giữa các yếu tố trong hình hoặc áp dụng sai công thức. Việc nhận biết và hiểu rõ các lỗi này sẽ giúp các em tính toán chính xác hơn và tránh sai sót trong các bài kiểm tra hoặc bài thi.
1. Nhầm lẫn giữa chiều cao và cạnh bên nghiêng:
Đây là lỗi phổ biến nhất. Học sinh thường chọn nhầm cạnh bên nghiêng làm chiều cao, trong khi chiều cao của hình thang vuông phải vuông góc với hai đáy.
Ví dụ: Trong hình thang vuông ABCD, nếu cạnh AD vuông góc với AB và CD thì AD mới là chiều cao, còn BC chỉ là cạnh bên nghiêng, không được dùng để thay vào công thức.
Cách khắc phục: Khi đọc đề, cần xác định đúng góc vuông trong hình. Cạnh nằm trong góc vuông nối giữa hai đáy chính là chiều cao cần dùng.
2. Sử dụng sai công thức hoặc quên chia đôi kết quả:
Một số học sinh chỉ nhớ mơ hồ công thức và viết sai thành S=(a + b) × h, bỏ mất phần chia 2, dẫn đến kết quả gấp đôi diện tích thật.
Công thức đúng luôn là: S=(a + b) × h / 2
Cách khắc phục: Học sinh có thể dùng mẹo ghi nhớ:
“ Đáy lớn cộng đáy nhỏ, nhân chiều cao chia hai” – vừa ngắn gọn vừa dễ thuộc, giúp tránh nhầm khi tính nhanh.
3. Nhập sai giá trị của các cạnh đáy:
Trong nhiều bài, học sinh nhầm lẫn giữa đáy lớn và đáy nhỏ, hoặc ghi sai đơn vị (cm, m, ...). Dù công thức không yêu cầu phân biệt thứ tự, nhưng sai đơn vị sẽ khiến kết quả sai lệch.
Cách khắc phục:
Ghi rõ ràng từng giá trị trước khi tính.
Kiểm tra lại đơn vị đo (ví dụ: nếu chiều cao tính bằng cm thì các đáy cũng phải là cm).
Nếu có thể, vẽ hình minh họa để tránh nhầm lẫn.
4. Không đổi đơn vị đo trước khi tính:
Khi bài toán cho các cạnh bằng những đơn vị khác nhau (như cm và m), học sinh thường quên đổi về cùng một đơn vị trước khi tính diện tích, dẫn đến kết quả sai hoàn toàn.
Ví dụ sai:
Đáy lớn=1 m, đáy nhỏ=50 cm, chiều cao=60 cm.
Nếu không đổi 1 m=100 cm thì công thức sẽ cho ra kết quả sai.
Cách khắc phục:
Luôn chuyển đổi tất cả đơn vị về cùng hệ đo trước khi thay số (thường là cm hoặc m).
5. Không xác định rõ hình là hình thang vuông:
Một số học sinh áp dụng công thức hình thang vuông cho mọi hình thang mà không kiểm tra xem hình có góc vuông hay không. Khi đó, chiều cao thực tế không nằm ở vị trí cạnh bên, khiến công thức bị sai.
Cách khắc phục:
Xác định dấu hiệu đặc trưng: có một cạnh bên vuông góc với hai đá
Nếu không có góc vuông, phải dựng đường cao hoặc sử dụng công thức hình thang thường thay vì công thức hình thang vuông.
6. Quên ghi đơn vị trong kết quả:
Dù tính toán đúng, nhưng nếu quên ghi đơn vị (cm² , m² , dm² , ...) thì bài vẫn bị trừ điểm.
Cách khắc phục:
Sau khi ra kết quả, luôn kiểm tra lại bước cuối:
“ Đơn vị đo của diện tích phải là đơn vị bình phương.”
Ví dụ: nếu đo cạnh bằng cm thì diện tích phải ghi là cm² .
7. Tính nhầm trung bình cộng hai đáy:
Một lỗi nhỏ nhưng hay gặp: cộng hai đáy rồi chia nhầm cho 3, hoặc quên chia 2, khiến kết quả sai lệch.
Cách khắc phục:
Nhớ rằng diện tích hình thang (kể cả hình thang vuông) luôn là trung bình cộng của hai đáy nhân với chiều cao.