Đường trung trực là gì
Đường trung trực của một đoạn thẳng là một khái niệm quan trọng trong hình học, thường được dùng để xác định các điểm có khoảng cách bằng nhau đến hai đầu mút của đoạn thẳng.
Định nghĩa:
Đường trung trực của đoạn thẳng AB là đường thẳng đi qua trung điểm của đoạn AB và vuông góc với đoạn thẳng đó. Nói cách khác, nếu gọi O là trung điểm của AB, thì đường thẳng trung trực của AB sẽ đi qua O và tạo với AB một góc vuông 90∘
Cách dựng đường trung trực:
Lấy đoạn thẳng AB.
Dùng compa vẽ hai cung tròn cùng bán kính, tâm lần lượt là A và B, sao cho hai cung này cắt nhau tại hai điểm C và D.
Nối hai điểm C và D, ta được đường trung trực của đoạn AB.
Tính chất quan trọng:
Mọi điểm nằm trên đường trung trực của đoạn thẳng AB đều cách đều hai đầu mút A và B, nghĩa là MA=MB.
Ngược lại, mọi điểm có khoảng cách bằng nhau đến A và B đều nằm trên đường trung trực của đoạn AB.
Trong tam giác, giao điểm của ba đường trung trực của ba cạnh là tâm đường tròn ngoại tiếp tam giác, tức là điểm cách đều ba đỉnh của tam giác.
Ý nghĩa hình học:
Đường trung trực giúp xác định vị trí cân bằng giữa hai điểm, là công cụ cơ bản trong việc dựng hình, chứng minh tính đối xứng, và giải các bài toán liên quan đến khoảng cách hay tâm đường tròn ngoại tiếp tam giác.
1. Đường trung trực của đoạn thẳng:
Giả sử ta có đoạn thẳng AB. Gọi M là trung điểm của AB, tức là AM=MB. Khi vẽ đường thẳng d đi qua M và vuông góc với AB, ta được đường trung trực của đoạn thẳng AB. Đặc điểm nổi bật là mọi điểm nằm trên đường trung trực này đều cách đều hai điểm A và B. Ví dụ, nếu lấy một điểm P bất kỳ trên d thì ta luôn có PA=PB. Đây là cơ sở để ta dùng đường trung trực trong việc dựng hình, xác định điểm cách đều hai điểm cho trước, hoặc vẽ đường tròn đi qua A và B.
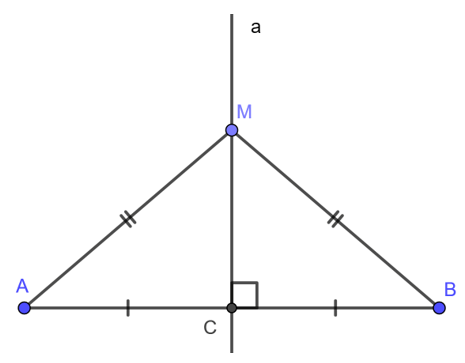
Trong tam giác
2. Đường trung trực trong tam giác:
Cho tam giác ABC, ta có thể vẽ ba đường trung trực lần lượt của ba cạnh BC, CA và AB. Chẳng hạn, đường trung trực của cạnh BC là đường thẳng đi qua trung điểm M của BC và vuông góc với BC tại M. Tương tự với hai cạnh còn lại. Ba đường trung trực này không song song mà sẽ cắt nhau tại một điểm O. Điểm O gọi là tâm đường tròn ngoại tiếp tam giác ABC, là điểm cách đều ba đỉnh của tam giác, nghĩa là OA=OB=OC. Khi vẽ đường tròn tâm O, bán kính OA, ta sẽ được đường tròn ngoại tiếp tam giác ABC.
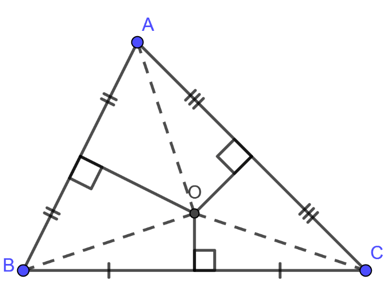
Đường trung trực trong tam giác
3. Đường trung trực trong hình chữ nhật:
Xét hình chữ nhật ABCD có hai cặp cạnh đối diện song song và bằng nhau. Đường trung trực của cạnh AB đồng thời cũng là đường trung trực của cạnh CD, vì hai cạnh này song song và có cùng độ dài. Tương tự, đường trung trực của AD cũng là của BC. Hai đường trung trực này cắt nhau tại tâm O – chính là giao điểm của hai đường chéo AC và BD. Điểm O là trung điểm của mỗi đường chéo, đồng thời cách đều bốn đỉnh A, B, C, D. Vì vậy, trong hình chữ nhật, các đường trung trực giúp xác định tâm hình rất dễ dàng.
4. Đường trung trực trong hình vuông:
Hình vuông là trường hợp đặc biệt của hình chữ nhật có bốn cạnh bằng nhau và bốn góc vuông. Trong hình vuông ABCD, mỗi đường trung trực của một cạnh vừa là trục đối xứng, vừa đồng thời là đường vuông góc chia cạnh đó thành hai phần bằng nhau. Ngoài ra, hai đường chéo của hình vuông cũng là hai đường trung trực của các cạnh đối diện. Tất cả các đường trung trực trong hình vuông đều cắt nhau tại tâm O – điểm giao của hai đường chéo. Tâm O này cách đều bốn đỉnh, và cũng là tâm đường tròn ngoại tiếp hình vuông.
Tính chất cơ bản của đường trung trực:
a. Mỗi điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
Giả sử ta có đoạn thẳng AB và đường trung trực d của nó. Với bất kỳ điểm M nằm trên đường trung trực d, ta luôn có MA=MB. Lý do là vì d vuông góc với AB tại trung điểm M₀ nên tam giác AMM₀ và BMM₀ là hai tam giác vuông có cạnh huyền và một cạnh góc vuông bằng nhau. Do đó, chúng bằng nhau theo trường hợp cạnh – góc vuông – cạnh huyền (g.c.g), suy ra MA=MB.
Tính chất này cho thấy đường trung trực chính là quỹ tích của những điểm cách đều hai đầu mút. Nói cách khác, nếu ta lấy tất cả các điểm mà khoảng cách tới A và B bằng nhau, nối lại thì chúng tạo thành đường trung trực của AB.
b. Ngược lại, điểm nào cách đều hai đầu mút của một đoạn thẳng thì điểm đó nằm trên đường trung trực của đoạn thẳng đó.
Nếu một điểm P bất kỳ thỏa mãn PA=PB thì P luôn nằm trên đường trung trực của AB. Để chứng minh, ta nối các đoạn thẳng PA, PB và nhận thấy rằng tam giác PAB là tam giác cân tại P (vì PA=PB). Khi dựng đường thẳng đi qua P và vuông góc với AB, ta thấy đường đó đi qua trung điểm của AB, tức là đường trung trực.
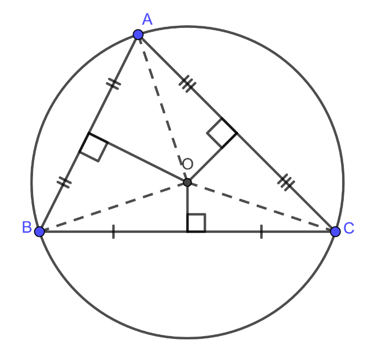
Điểm trung trực là tâm đường tròn
Hai tính chất này cùng nhau chứng minh mối quan hệ hai chiều: điểm nằm trên đường trung trực ⇔ điểm cách đều hai đầu mút của đoạn thẳng. Đây là cơ sở cho rất nhiều bài toán hình học về quỹ tích và dựng hình.
Hệ quả và ứng dụng trong hình học:
Trong tam giác: Ba đường trung trực của ba cạnh của một tam giác luôn cắt nhau tại một điểm duy nhất, gọi là tâm đường tròn ngoại tiếp tam giác (O). Từ tính chất trên, ta biết rằng O cách đều ba đỉnh của tam giác, tức là OA=OB=OC. Điều này giúp ta dễ dàng dựng được đường tròn đi qua ba đỉnh của tam giác – một ứng dụng rất phổ biến trong hình học phẳng.
Trong tam giác cân: Đường trung trực của cạnh đáy đồng thời là đường cao, đường trung tuyến và đường phân giác đi từ đỉnh xuống đáy. Tính chất đặc biệt này cho thấy tam giác cân có sự đối xứng qua đường trung trực của đáy.
Trong hình chữ nhật: Các đường trung trực của các cặp cạnh đối diện cắt nhau tại một điểm – chính là giao điểm của hai đường chéo. Điểm này gọi là tâm đối xứng của hình chữ nhật, và nó cách đều bốn đỉnh của hình.
Trong hình vuông: Các đường trung trực của các cạnh cũng đồng thời là các trục đối xứng và đường chéo của hình. Chúng gặp nhau tại tâm O – điểm cách đều bốn đỉnh. Vì vậy, tâm O cũng chính là tâm đường tròn ngoại tiếp hình vuông.
Ý nghĩa và vai trò của đường trung trực:
Đường trung trực có vai trò rất quan trọng trong hình học vì nó thể hiện tính cân bằng và đối xứng. Từ góc nhìn quỹ tích, đây là đường biểu diễn tập hợp các điểm cách đều hai đầu mút của một đoạn thẳng. Từ góc nhìn ứng dụng, nó giúp xác định tâm, vị trí đối xứng, và giải thích mối quan hệ giữa các yếu tố trong hình.
Trong thực tế, tính chất của đường trung trực còn được ứng dụng trong kỹ thuật, kiến trúc, thiết kế – chẳng hạn khi cần xác định vị trí trung tâm, cân đối trong bản vẽ hoặc cấu trúc.
Bài 1: Cho đoạn thẳng AB=8 cm. Hãy vẽ đường trung trực của AB và xác định một điểm P trên đường đó cách A 5 cm.
LỜI GIẢI: Vẽ đoạn AB dài 8 cm; tìm trung điểm M của AB (AM=MB=4 cm); vẽ đường thẳng d qua M vuông góc với AB — đó là đường trung trực; mọi điểm trên d đều thỏa PA=PB; để tìm P sao cho PA=5 cm, lấy tâm A bán kính 5 cm vẽ cung cắt d tại P (hoặc hai điểm P1, P2). Kiểm tra: PA=5 cm theo cách dựng, đồng thời PB=PA do P nằm trên đường trung trực.
Bài 2: Trong tam giác ABC, BC=10 cm. Vẽ đường trung trực của BC và chứng minh rằng mọi điểm trên đường này cách đều B và C.
LỜI GIẢI: Trên cạnh BC lấy trung điểm M (BM=MC=5 cm); vẽ đường d qua M vuông góc BC; với điểm bất kỳ P ∈ d nối PB, PC; tam giác PBM và PCM có BM=CM, PM chung, góc PMB=PMC=90° ⇒ hai tam giác vuông bằng nhau theo cạnh-góc-cạnh ⇒ PB=PC. Vậy mọi điểm nằm trên d cách đều B và C.
Bài 3: Cho tam giác ABC cân tại A (AB=AC). Chứng minh đường trung trực của BC đồng thời là đường cao, đường trung tuyến và đường phân giác từ A xuống BC.
LỜI GIẢI: Vì tam giác cân AB=AC nên trung điểm M của BC có AM là trục đối xứng: khi vẽ đường trung trực d của BC (qua M và vuông góc BC) thì d đi qua A (do đối xứng) ⇒ d chính là đường AM. Do d vuông góc BC nên AM là đường cao; do M là trung điểm nên AM là đường trung tuyến; do đối xứng nên AM là đường phân giác. Kết luận: đường trung trực của BC (tức AM) là đường cao, trung tuyến và phân giác từ A.
Bài 4: Cho hình chữ nhật ABCD. Chỉ ra vị trí giao điểm của các đường trung trực của các cạnh và nêu tính chất của điểm đó.
LỜI GIẢI: Trong hình chữ nhật các cặp cạnh đối diện song song và bằng nhau; đường trung trực của AB trùng với đường trung trực của CD, đường trung trực của AD trùng với đường trung trực của BC; hai đường trung trực này cắt nhau tại O, O là giao điểm hai đường chéo; O cách đều bốn đỉnh (OA=OB=OC=OD). Vì vậy O là tâm đối xứng và tâm đường tròn ngoại tiếp hình chữ nhật.
Bài 5: Cho đoạn thẳng AB. Hãy miêu tả và dựng quỹ tích các điểm P sao cho PA − PB=0 và giải thích vì sao đó là đường trung trực.
LỜI GIẢI: Điều kiện PA − PB=0 tương đương PA=PB, tức tập hợp các điểm có khoảng cách đến A và B bằng nhau. Quỹ tích này là một đường thẳng vuông góc với AB đi qua trung điểm M của AB, tức đường trung trực. Dựng: tìm M rồi vẽ d qua M vuông góc AB. Mọi P ∈ d thoả PA=PB.
Bài 6: Cho tam giác ABC với AB=6 cm, AC=8 cm, BC=10 cm. (a) Vẽ các đường trung trực của AB và AC; (b) Tìm giao điểm O của hai đường trung trực đó và chứng minh OA=OB=OC.
LỜI GIẢI: (a) Trên AB lấy trung điểm M1 (3 cm) và vẽ d1 qua M1 vuông góc AB; trên AC lấy trung điểm M2 (4 cm) và vẽ d2 qua M2 vuông góc AC. (b) Giao điểm O=d1 ∩ d2. Vì O nằm trên đường trung trực d1 nên OA=OB; vì O nằm trên d2 nên OA=OC. Từ OA=OB và OA=OC suy ra OA=OB=OC, nên O là tâm đường tròn ngoại tiếp tam giác ABC.