Tâm đường tròn ngoại tiếp tam giác
Trong hình học, tam giác là một trong những hình học cơ bản nhưng lại có rất nhiều tính chất quan trọng, đặc biệt liên quan đến đường tròn ngoại tiếp. Việc hiểu rõ tâm đường tròn ngoại tiếp tam giác không chỉ giúp học sinh giải các bài toán hình học một cách nhanh chóng, chính xác mà còn ứng dụng trong kiến trúc, kỹ thuật và thiết kế.
Bài viết này sẽ giải thích chi tiết: đường tròn ngoại tiếp tam giác là gì, cách xác định tâm, các tính chất của tâm, và nêu ứng dụng thực tế của tâm đường tròn ngoại tiếp
Đường tròn ngoại tiếp tam giác là đường tròn đi qua cả ba đỉnh của tam giác.
Tâm đường tròn ngoại tiếp là điểm cách đều ba đỉnh của tam giác, gọi là O.
Bán kính đường tròn ngoại tiếp (R) là khoảng cách từ tâm O đến bất kỳ đỉnh nào của tam giác.
Ví dụ minh họa
Tam giác ABC, có ba đỉnh A, B, C. Đường tròn đi qua A, B, C có tâm O và bán kính R=OA=OB=OC.
Khi vẽ hình, bạn sẽ thấy ba điểm đỉnh của tam giác nằm trên một đường tròn duy nhất, và tâm O là tâm đối xứng của ba đỉnh.
Lưu ý
Mỗi tam giác chỉ có một đường tròn ngoại tiếp duy nhất.
Đường tròn ngoại tiếp tam giác đều tồn tại với tam giác nhọn, tam giác vuông, tam giác tù.

Đường tròn ngoại tiếp tam giácTâm đường tròn ngoại tiếp được tìm bằng cách xác định giao điểm của ba đường trung trực của tam giác.
Bước 1: Xác định đường trung trực
Đường trung trực là đường vuông góc với một cạnh tại trung điểm của cạnh đó.
Với tam giác ABC, vẽ trung trực của ít nhất hai cạnh (ví dụ AB và AC).
Bước 2: Xác định giao điểm
Giao điểm của hai đường trung trực này chính là tâm O của đường tròn ngoại tiếp tam giác.
Khi vẽ thêm trung trực thứ ba, nó cũng đi qua giao điểm này, xác nhận đúng tâm.
Bước 3: Xác định bán kính
Bán kính R=khoảng cách từ tâm O đến một đỉnh của tam giác (OA, OB hoặc OC).
Ví dụ minh họa
Cho tam giác ABC:
Tìm trung điểm M của AB, vẽ đường trung trực AB.
Tìm trung điểm N của AC, vẽ đường trung trực AC.
Giao điểm của hai đường trung trực là O, tâm đường tròn ngoại tiếp.
Bán kính R=OA=OB=OC.
Công thức tínhTâm cách đều ba đỉnh
Tâm O nằm cách đều ba đỉnh của tam giác, nghĩa là:
OA=OB=OC=R
Đây là tính chất cơ bản nhất và cũng là đặc trưng nhận biết tâm đường tròn ngoại tiếp.
Vị trí của tâm tùy theo loại tam giác
Tam giác nhọn: Tâm O nằm bên trong tam giác.
Tam giác vuông: Tâm O nằm trên trung điểm của cạnh huyền.
Tam giác tù: Tâm O nằm bên ngoài tam giác.
Giao điểm của các đường trung trực
Tâm O là giao điểm duy nhất của ba đường trung trực của tam giác.
Tính chất này được sử dụng để vẽ đường tròn ngoại tiếp và xác định bán kính.
Liên hệ với bán kính
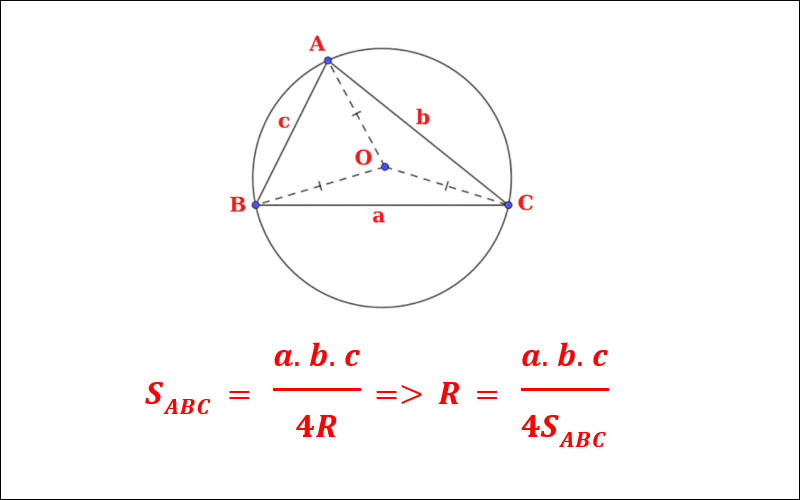
Bán kính đường tròn ngoại tiếp R được tính bằng công thức:
R=(abc) / (4S)
Trong đó:
a, b, c: độ dài các cạnh tam giác
S: diện tích tam giác
Công thức này đặc biệt hữu ích khi chỉ biết độ dài các cạnh mà không cần vẽ đường trung trực.

Giờ học toánTrong học tập và giải toán
Giúp học sinh vẽ chính xác đường tròn ngoại tiếp.
Dùng trong bài toán tính bán kính, khoảng cách, diện tích tam giác, hoặc các bài toán hình học nâng cao.
Liên quan đến đường trung trực, đường cao, đường phân giác, giúp phân tích tam giác phức tạp.
Trong kiến trúc và xây dựng
Xác định tâm đường tròn giúp thiết kế cầu vòm, mái cong, vòng cung chính xác.
Hỗ trợ tạo các hình dạng đối xứng cho cửa sổ, mái nhà, và chi tiết trang trí.
Trong kỹ thuật và thiết kế cơ khí
Khi chế tạo các chi tiết có hình tròn đi qua ba điểm cố định, tâm đường tròn ngoại tiếp được sử dụng để xác định vị trí và bán kính.
Giúp vẽ bản vẽ chính xác, đảm bảo các bộ phận cơ khí lắp khít.
Trong đồ họa và thiết kế
Dùng để vẽ các tam giác và đường tròn ngoại tiếp trong thiết kế logo, mô hình 3D, hoặc các ứng dụng phần mềm CAD.
Đảm bảo các điểm đỉnh cân bằng và đối xứng theo tâm O.
Ví dụ 1: Xác định tâm đường tròn ngoại tiếp tam giác nhọn
Tam giác ABC có các cạnh AB=5 cm, AC=6 cm, BC=7 cm.
Xác định trung điểm AB, AC, vẽ đường trung trực → giao điểm là O.
Bán kính: đo OA=OB=OC=khoảng cách từ O đến đỉnh → dùng công thức R=(abc)/(4S).
Ví dụ 2: Tâm đường tròn ngoại tiếp tam giác vuông
Tam giác vuông ABC, vuông tại A.
Cạnh huyền BC=10 cm.
Tâm O nằm trên trung điểm BC, bán kính R=5 cm.
Ví dụ 3: Tâm đường tròn ngoại tiếp tam giác tù
Tam giác DEF, góc tại D > 90° .
Tâm O nằm bên ngoài tam giác, khoảng cách từ O đến các đỉnh bằng nhau → vẽ được đường tròn ngoại tiếp.
Bài tập luyện tập
Tam giác GHI có các cạnh: GH=6 cm, HI=8 cm, GI=10 cm. Tìm tâm đường tròn ngoại tiếp và bán kính.
Vẽ tam giác vuông JKL, vuông tại J, cạnh huyền KL=12 cm. Xác định tâm đường tròn ngoại tiếp.
Cho tam giác nhọn MNO, các đỉnh cách nhau 5 cm, 6 cm, 7 cm. Xác định vị trí tâm đường tròn ngoại tiếp và bán kính.
Mẹo Nhớ Khi Xác Định Tâm Đường Tròn Ngoại Tiếp
Dùng đường trung trực: Giao điểm của ba đường trung trực luôn là tâm O.
Nhớ vị trí tùy loại tam giác:
Nhọn: trong tam giác
Vuông: trên trung điểm cạnh huyền
Tù: ngoài tam giác
Sử dụng công thức bán kính: R=(abc)/(4S) nếu biết độ dài các cạnh.
Thực hành vẽ: Vẽ nhiều loại tam giác và đường tròn ngoại tiếp để nhận biết trực quan.
Đường tròn ngoại tiếp tam giác là đường tròn đi qua cả ba đỉnh của tam giác, với tâm đường tròn ngoại tiếp O cách đều ba đỉnh.
Cách xác định tâm: giao điểm của ba đường trung trực.
Tính chất: O cách đều ba đỉnh, vị trí tùy thuộc loại tam giác, liên hệ trực tiếp với bán kính R.
Ứng dụng: học tập (vẽ tam giác, tính bán kính), kiến trúc (mái vòm, cửa sổ), kỹ thuật, đồ họa.
Thực hành nhiều ví dụ và bài tập giúp học sinh, sinh viên và người làm kỹ thuật nắm vững lý thuyết, tính toán chính xác, và ứng dụng linh hoạt trong thực tế.
Hiểu rõ tâm đường tròn ngoại tiếp giúp phát triển tư duy hình học, kỹ năng vẽ, và áp dụng vào các bài toán thực tế, từ đó nâng cao khả năng phân tích và giải quyết vấn đề trong toán học và đời sống.