Tâm đường tròn ngoại tiếp tam giác
Trong hình học, tam giác là một trong những hình cơ bản, được nghiên cứu từ cấp tiểu học đến đại học. Khi nghiên cứu tam giác, học sinh sẽ tiếp xúc với khái niệm đường tròn ngoại tiếp.
Tâm đường tròn ngoại tiếp tam giác là gì?
Tâm đường tròn ngoại tiếp tam giác là điểm nằm cách đều ba đỉnh của tam giác, từ đó vẽ được đường tròn đi qua cả ba đỉnh. Nói cách khác, tâm đường tròn ngoại tiếp là giao điểm của ba đường trung trực của tam giác.
Khái niệm này quan trọng không chỉ trong hình học lý thuyết mà còn ứng dụng trong các bài toán thiết kế, kiến trúc, xây dựng, đồ họa, định vị và nhiều lĩnh vực thực tế khác.
Tâm đường tròn ngoại tiếp có nhiều tính chất đặc biệt giúp học sinh dễ nhận biết và áp dụng trong bài tập:
Giao điểm của các đường trung trực
Ba đường trung trực của tam giác luôn đồng quy tại một điểm
Điểm đồng quy này chính là tâm đường tròn ngoại tiếp
Đường trung trực là đường thẳng vuông góc với cạnh tam giác tại trung điểm của cạnh đó
Cách đều các đỉnh
Tâm đường tròn ngoại tiếp cách đều ba đỉnh của tam giác
Khoảng cách từ tâm đến mỗi đỉnh là bán kính của đường tròn ngoại tiếp
Vị trí tùy thuộc vào loại tam giác
Tam giác nhọn: tâm nằm bên trong tam giác
Tam giác vuông: tâm nằm tại trung điểm cạnh huyền
Tam giác tù: tâm nằm bên ngoài tam giác
Tính chất hình học bổ sung
Từ tâm đường tròn ngoại tiếp, kéo bán kính đến các đỉnh tạo thành ba đoạn thẳng bằng nhau
Hình tròn ngoại tiếp luôn tồn tại duy nhất cho mỗi tam giác
Hiểu rõ các tính chất này giúp học sinh xác định tâm đường tròn ngoại tiếp một cách nhanh chóng, từ đó áp dụng vào các bài toán vẽ hình, tính bán kính hoặc áp dụng vào các bài toán thực tế.
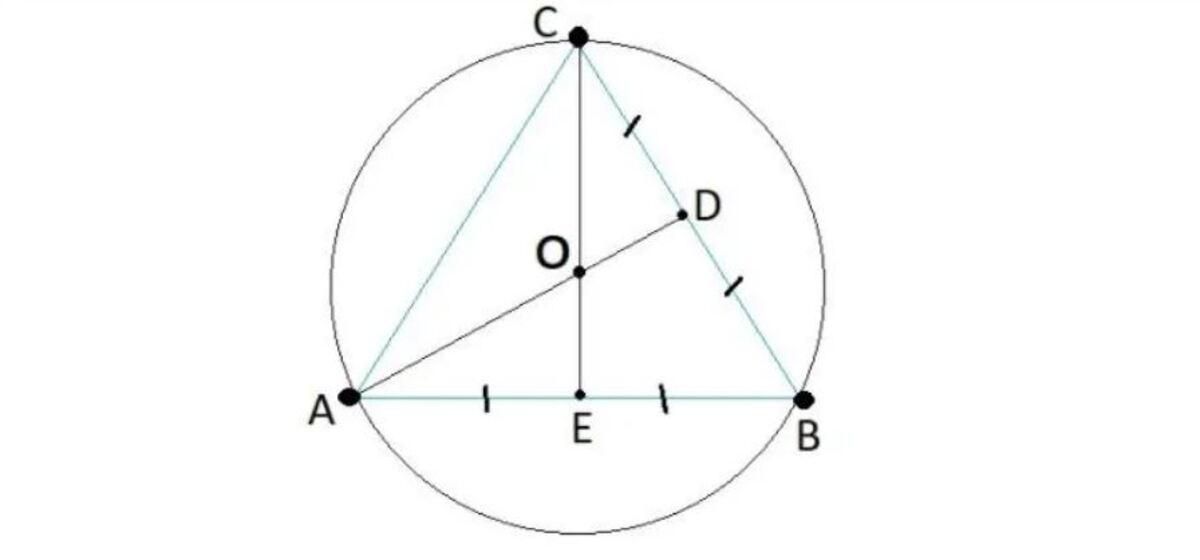Đường tròn ngoại tiếp tam giácĐể xác định tâm đường tròn ngoại tiếp, có nhiều phương pháp. Hai phương pháp phổ biến nhất là dùng đường trung trực hoặc tọa độ trong mặt phẳng Oxy.
Xác định tâm bằng giao điểm ba đường trung trực
Bước 1: Vẽ ba đường trung trực của các cạnh tam giác
Đường trung trực là đường vuông góc với cạnh tại trung điểm của cạnh đó
Bước 2: Tìm giao điểm của hai trong ba đường trung trực
Giao điểm này chính là tâm đường tròn ngoại tiếp
Vì ba đường đồng quy, nên giao điểm của hai đường là điểm chung của cả ba đường
Bước 3: Kẻ bán kính từ tâm đến một đỉnh bất kỳ
Khoảng cách từ tâm đến đỉnh là bán kính đường tròn ngoại tiếp
Xác định tâm trong hệ tọa độ Oxy
Cho tam giác có các đỉnh A(x1, y1), B(x2, y2), C(x3, y3)
Trung điểm AB: M=((x1+x2)/2, (y1+y2)/2)
Hệ số góc AB: k1=(y2-y1)/(x2-x1)
Hệ số góc đường trung trực: k1' =-1/k1
Phương trình đường trung trực AB: y - My=k1' * (x - Mx)
Tương tự, xác định đường trung trực BC
Giao điểm của hai phương trình đường trung trực chính là tâm đường tròn ngoại tiếp
Phương pháp này hữu ích khi làm bài tập tọa độ hoặc bài toán hình học phẳng nâng cao.
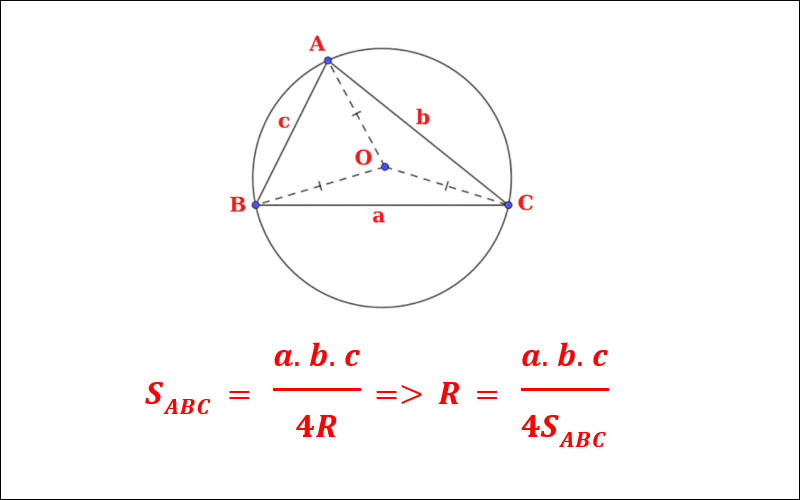Công thức tính bán kínhSau khi xác định tâm, bán kính đường tròn ngoại tiếp được tính bằng khoảng cách từ tâm đến một đỉnh bất kỳ.
Công thức khoảng cách
Cho tâm O(x0, y0) và đỉnh A(x1, y1):
R=√ ((x1 - x0)² + (y1 - y0)² )
Trong đó:
R: bán kính đường tròn ngoại tiếp
(x0, y0): tọa độ tâm đường tròn
(x1, y1): tọa độ đỉnh tam giác
Công thức bán kính theo cạnh tam giác
Với tam giác có các cạnh a, b, c (đối diện với các đỉnh A, B, C) và diện tích S tam giác:
R=(a * b * c) / (4 * S)
a, b, c: độ dài ba cạnh
S: diện tích tam giác (có thể tính bằng công thức Heron)
S=√ (p(p-a)(p-b)(p-c)), p=(a+b+c)/2
Ví dụ: Tam giác có các cạnh a=5, b=6, c=7
Tính nửa chu vi: p=(5+6+7)/2=9
Diện tích: S=√ (9*(9-5)(9-6)(9-7))=√ (943*2)=√ 216 ≈ 14.7
Bán kính: R=(567)/(4*14.7)=210/58.8 ≈ 3.57
Trong hình học
Giúp vẽ đường tròn ngoại tiếp chính xác
Giải các bài toán về tính bán kính, khoảng cách, đối xứng trong tam giác
Hỗ trợ chứng minh các định lý hình học phẳng nâng cao
Trong đời sống thực tế
Kiến trúc:Vẽ các vòng cung hoặc thiết kế mái vòm theo hình tam giác
Đồ họa và thiết kế: Tạo các đối xứng và bố cục cân đối dựa trên tam giác và đường tròn ngoại tiếp
Bản đồ và định vị: Xác định tâm vị trí sao cho khoảng cách từ điểm đến các trục điểm cố định bằng nhau
Trong toán học ứng dụng
Sử dụng trong lập trình máy tính, mô phỏng hình học, robot định vị
Ứng dụng trong thiết kế cơ khí, tính toán vị trí tối ưu
Học sinh trong giờ toánBài tập 1: Xác định tâm đường tròn ngoại tiếp nhọn
Cho tam giác ABC với các đỉnh A(1, 2), B(5, 6), C(7, 2).
Hỏi tọa độ tâm đường tròn ngoại tiếp ?
Hướng dẫn giải:
Xác định phương trình đường trung trực AB và BC
Giải hệ phương trình để tìm giao điểm → tọa độ tâm O
Tính bán kính R=khoảng cách từ O đến A
Bài tập 2: Tính bán kính đường tròn ngoại tiếp tam giác
Cho tam giác có các cạnh a=6, b=8, c=10
Tính diện tích: S=√ (p(p-a)(p-b)(p-c)), p=(6+8+10)/2=12
S=√ (12*(12-6)(12-8)(12-10))=√ (1264*2)=√ 576=24
Bán kính: R=(abc)/(4S)=(6810)/(424)=480/96=5
Tâm đường tròn ngoại tiếp là điểm đồng quy của ba đường trung trực, cách đều ba đỉnh của tam giác. Hiểu rõ khái niệm, tính chất, cách xác định và công thức tính bán kính giúp học sinh:
Vẽ hình chính xác
Giải bài toán liên quan đến tam giác và đường tròn ngoại tiếp
Áp dụng vào các bài toán thực tế như kiến trúc, thiết kế đồ họa, định vị