Góc tù bao nhiêu độ?
Trong hình học, góc là một trong những khái niệm cơ bản và phổ biến nhất, được sử dụng trong các bài toán từ cấp tiểu học đến đại học. Góc tù là một loại góc đặc biệt với các tính chất riêng, có ứng dụng rộng rãi trong học tập và đời sống thực tế.
Góc tù bao nhiêu độ?
Góc tù là góc lớn hơn 90 độ nhưng nhỏ hơn 180 độ. Nói cách khác:
90° < góc tù < 180°
Góc tù xuất hiện nhiều trong các bài toán hình học về tam giác, tứ giác, đa giác và các hình học phẳng khác. Việc nắm vững kiến thức về góc tù bao nhiêu độ sẽ giúp học sinh dễ dàng nhận biết các loại góc, tính toán trong tam giác tù, và giải các bài toán liên quan đến đo đạc hoặc xây dựng.
 Góc tù trong toán học
Góc tù trong toán họcViệc nhận biết góc tù không khó nếu bạn nắm vững các dấu hiệu và cách quan sát:
Quan sát trực tiếp bằng thước đo góc
Sử dụng thước đo góc (protractor) để đo góc.
Nếu góc lớn hơn 90 độ nhưng chưa đến 180 độ, đó là góc tù.
Ví dụ: góc 120° là một góc tù, còn góc 85° là góc nhọn, 180° là góc bẹt.
Dựa vào đặc điểm hình học
Góc tù thường mở rộng hơn góc vuông, tức là khi vẽ bằng compa hoặc thước, bạn sẽ thấy cạnh thứ hai " nhô ra" nhiều hơn so với góc vuông.
Trong tam giác, nếu một góc của tam giác lớn hơn 90° , tam giác đó được gọi là tam giác tù, và góc lớn đó chính là góc tù.
Nhận biết qua mối quan hệ với các góc khác
Trong tam giác, tổng ba góc luôn bằng 180° . Nếu một góc là góc tù, hai góc còn lại phải là góc nhọn, vì tổng không vượt quá 180° .
Trong hình tứ giác hoặc đa giác, bạn có thể xác định góc tù bao nhiêu độ bằng cách dựa vào tổng các góc nội tiếp của hình.
Dấu hiệu nhận biết trực quan
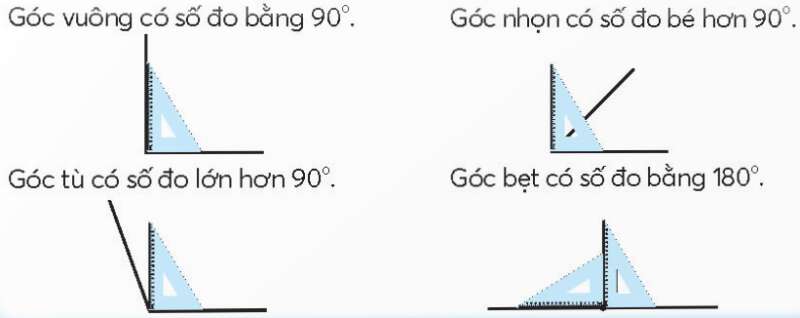
Góc nhọn < 90°
Góc vuông=90°
Góc tù > 90° và < 180°
Góc bẹt=180°
Việc phân biệt này giúp học sinh nhanh chóng xác định loại góc khi nhìn hình mà không cần đo chính xác.
 Số đo của góc tù
Số đo của góc tùGóc tù bao nhiêu độ không chỉ xuất hiện trong sách giáo khoa mà còn có nhiều ứng dụng thực tế.
Trong học tập
Hình học phẳng: Xác định góc tù giúp phân loại tam giác (tam giác nhọn, tam giác vuông, tam giác tù).
Chứng minh định lý: Nhiều định lý về tam giác, tứ giác, đa giác sử dụng khái niệm góc tù để chứng minh tính chất hoặc quan hệ giữa các cạnh và góc.
Dựng hình: Khi vẽ tam giác tù, góc tù phải được xác định chính xác để các cạnh còn lại vẽ đúng tỷ lệ.
Trong đời sống thực tế
Kiến trúc và xây dựng: Các góc tù xuất hiện trong mái nhà, đường dốc, các chi tiết thiết kế. Kỹ sư và kiến trúc sư cần tính toán chính xác để đảm bảo kết cấu chắc chắn.
Đồ họa và thiết kế: Khi thiết kế các chi tiết có hình học phức tạp, góc tù giúp tạo ra các hình ảnh thẩm mỹ, cân đối.
Đo đạc và định vị: Trong khảo sát địa hình hoặc lắp đặt các vật thể, việc nhận biết góc tù giúp xác định khoảng cách và hướng đúng, tránh lỗi trong thi công.
Như vậy, việc hiểu và nhận biết góc tù bao nhiêu độ không chỉ giúp học sinh học tốt hình học mà còn phát triển tư duy không gian và kỹ năng thực hành trong nhiều lĩnh vực.
Để nắm chắc kiến thức về góc tù, việc thực hành là rất quan trọng. Dưới đây là một số bài tập minh họa cùng hướng dẫn giải chi tiết:
Bài tập 1: Xác định góc tù trong tam giác
Cho tam giác ABC với các góc: A=120° , B=30° , C=30° .
Hỏi góc nào là góc tù?
Hướng dẫn giải:
Góc A=120° > 90° → là góc tù.
Góc B=30° < 90° → góc nhọn
Góc C=30° < 90° → góc nhọn
Kết luận: Góc A là góc tù.
Bài tập 2: Xác định tam giác tù
Tam giác XYZ có các góc: X=50° , Y=100° , Z=30° .
Hỏi đây là loại tam giác nào?
Hướng dẫn giải:
Góc Y=100° > 90° → tam giác tù, vì chỉ cần một góc lớn hơn 90° là tam giác được gọi là tam giác tù.
Các góc khác < 90° → nhọn
Tổng ba góc: 50+100+30=180° → đúng.
Kết luận: Tam giác XYZ là tam giác tù với góc tù tại Y.
Bài tập 3: Tính góc còn lại khi biết một góc tù
Cho tam giác DEF có một góc tù D=140° và góc E=25° . Tính góc F.
Hướng dẫn giải:
Tổng ba góc trong tam giác=180°
Góc F=180° - D - E=180° - 140° - 25° =15°
Kết luận: Góc F=15° (góc nhọn), tam giác có một góc tù D=140° .
Bài tập 4: Nhận biết góc tù trong hình vẽ
Cho hình tứ giác ABCD, biết góc A=110° , góc B=70° , góc C=90° , góc D=?.
Xác định góc D và nhận biết các góc tù.
Hướng dẫn giải:
Tổng bốn góc trong tứ giác=360°
Góc D=360° - (A + B + C)=360° - (110 + 70 + 90)=90°
Góc A=110° → góc tù
Góc D=90° → góc vuông
Kết luận: Trong tứ giác này, góc A là góc tù, góc D là góc vuông.
 Dạy học sinh cách nhận biết
Dạy học sinh cách nhận biếtGóc tù luôn lớn hơn 90° nhưng nhỏ hơn 180° .
Trong tam giác, chỉ có thể có một góc tù vì tổng ba góc=180° .
Sử dụng thước đo góc hoặc quan sát hình học để xác định nhanh loại góc.
Khi làm bài toán thực tế, luôn kiểm tra tổng các góc để đảm bảo chính xác.
Góc tù là một khái niệm cơ bản nhưng quan trọng trong hình học, với các đặc điểm sau:
Góc tù lớn hơn 90° và nhỏ hơn 180°
Góc tù xuất hiện trong tam giác tù, tứ giác, đa giác
Có nhều ứng dụng trong học tập, dựng hình, kiến trúc, đo đạc và thiết kế
Nhận biết góc tù bằng thước đo, quan sát hình học và phân loại góc dựa vào các dấu hiệu cơ bản
Nắm vững kiến thức về góc tù giúp học sinh:
Xác định đúng loại tam giác, góc trong các bài toán hình học
Giải bài tập nhanh và chính xác
Phát triển tư duy không gian và áp dụng vào các lĩnh vực thực tế