Công thức tính diện tích xung quanh hình trụ
Trong hình học không gian, hình trụ là khối hình quen thuộc và thường xuyên xuất hiện trong chương trình học cũng như trong đời sống. Từ những chiếc lon nước giải khát, ống nước cho đến các bể chứa đều mang dáng dấp của hình trụ. Khi học về hình trụ, học sinh thường gặp câu hỏi liên quan đến diện tích bề mặt. Trong đó, công thức tính diện tích xung quanh hình trụ là kiến thức cơ bản cần nắm vững trước khi tìm hiểu các dạng mở rộng như diện tích toàn phần hoặc thể tích.
Diện tích xung quanh hình trụchính là phần diện tích bao phủ mặt cong của hình. Hãy tưởng tượng khi bóc lớp giấy dán quanh một chiếc lon nước, bạn sẽ thu được một hình chữ nhật. Chính diện tích của hình chữ nhật đó chính là diện tích xung quanh hình trụ. Việc hiểu được bản chất này giúp cho công thức trở nên dễ nhớ và dễ áp dụng hơn.
Tầm quan trọng của việc học công thức
Công thức này không chỉ giúp giải các bài tập hình học ở trường mà còn có giá trị thực tế rất lớn. Khi tính toán lượng sơn để phủ bên ngoài một ống nước, khi ước lượng lớp giấy cần dán quanh một lon sữa hay khi đo diện tích lớp kim loại cần dùng để chế tạo một trụ rỗng, tất cả đều liên quan trực tiếp đến diện tích xung quanh hình trụ.
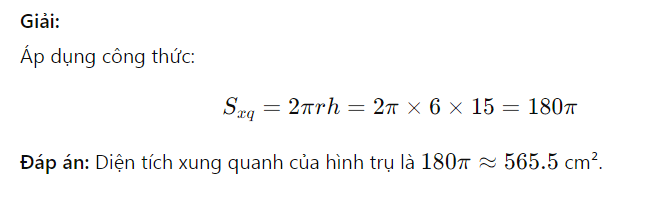
Công thức tính diện tích xung quanh của hình trụĐể nắm chắc kiến thức, bạn cần hiểu cách hình thành công thức thay vì chỉ học thuộc lòng.
Công thức cơ bản
Diện tích xung quanh hình trụ được tính theo công thức:
Sxq= 2πrh
Trong đó rlà bán kính đáy của hình trụ, hlà chiều cao, πlà số pi có giá trị xấp xỉ 3, 14.
Giải thích công thức
Khi tưởng tượng cắt hình trụ dọc theo một đường sinh rồi trải mặt cong ra, bạn sẽ thu được một hình chữ nhật có chiều dài bằng chu vi đáy 2πrvà chiều rộng bằng chiều cao h. Diện tích hình chữ nhật này chính là 2πrh. Vì vậy, công thức không hề khó nhớ nếu bạn liên hệ trực quan như vậy.
Phân biệt với diện tích toàn phần
Ngoài diện tích xung quanh, hình trụ còn có diện tích toàn phần bao gồm cả hai đáy. Công thức diện tích toàn phần là Stp =2πrh+2πr² . Sự phân biệt này giúp bạn tránh nhầm lẫn khi làm bài tập, vì có nhiều đề bài chỉ yêu cầu phần xung quanh chứ không tính cả hai đáy.
Bài toán hình trụ với bán kính và chiều cao cụ thểLý thuyết sẽ dễ nhớ hơn nhiều khi đi kèm với ví dụ cụ thể.
Ví dụ 1
Một hình trụ có bán kính đáy r=5 cm và chiều cao h=10 cm. Hãy tính diện tích xung quanh.
Lời giải: Sxq =2πrh=2 × 3, 14 × 5 × 10=314 cm² .
Ví dụ 2
Một lon nước ngọt có hình dạng hình trụ với đường kính đáy 6 cm và chiều cao 12 cm. Tính diện tích xung quanh lon nước.
Lời giải: Bán kính r=3 cm. Sxq=2πrh=2 × 3, 14 × 3 × 12=226, 08 cm² .
Ví dụ 3
Một bể chứa dạng hình trụ có bán kính 0, 8 m và chiều cao 2 m. Người ta muốn sơn phần mặt cong bên ngoài bể. Hãy tính diện tích cần sơn.
Lời giải: Sxq =2πrh=2 × 3, 14 × 0, 8 × 2=10, 05 m² .
Tính diện tích giấy dán quanh lon nước dạng hình trụKhi học sinh thực hành, có một số lỗi thường gặp cần được lưu ý. Trước hết là nhầm lẫn giữa bán kính và đường kính. Đề bài có thể cho đường kính, khi đó bạn cần chia đôi để tìm bán kính trước khi đưa vào công thức.
Một lỗi khác là quên đổi đơn vị đo. Nếu chiều cao tính bằng mét mà bán kính tính bằng cm thì kết quả diện tích sẽ sai. Do đó, cần đổi về cùng một đơn vị trước khi tính toán.
Ngoài ra, học sinh đôi khi nhầm lẫn diện tích xung quanh với diện tích toàn phần. Để tránh nhầm, hãy nhớ diện tích xung quanh chỉ bao gồm mặt cong, trong khi diện tích toàn phần tính cả hai đáy.
Trong thực tế, nhiều bài toán yêu cầu tính toán vật liệu như giấy dán, lớp sơn hay màng bọc. Khi gặp những bài như vậy, bạn hãy hình dung phần diện tích cần tính có bao gồm nắp và đáy hay chỉ phần thân, từ đó áp dụng công thức đúng.
Vai trò của việc hiểu bản chất
Khi đã nắm được rằng diện tích xung quanh hình trụ thực chất là diện tích hình chữ nhật có một cạnh bằng chu vi đáy và một cạnh bằng chiều cao, bạn sẽ thấy công thức trở nên dễ thuộc hơn nhiều. Hiểu bản chất cũng giúp bạn linh hoạt xử lý các biến đổi của đề bài, chẳng hạn như khi đề cho đường kính thay vì bán kính hoặc khi cần tính ngược lại chiều cao từ diện tích đã biết.
Qua bài viết này, bạn đã nắm vững công thức tính diện tích xung quanh hình trụ cùng với cách giải thích và ví dụ minh họa chi tiết. Đây là kiến thức quan trọng trong hình học không gian, không chỉ giúp làm tốt các bài tập trên lớp mà còn có ứng dụng thực tiễn trong đời sống.
Hãy luyện tập thêm nhiều dạng bài để rèn khả năng áp dụng công thức. Việc luyện tập thường xuyên sẽ giúp bạn tự tin hơn trong các kỳ kiểm tra cũng như khi gặp những bài toán ứng dụng thực tế. Quan trọng hơn, hãy luôn nhớ kiểm tra đơn vị và xác định chính xác yêu cầu đề bài để không bị nhầm lẫn giữa diện tích xung quanh và diện tích toàn phần.
Trên đây là một số thông tin về chủ đề công thức tính diện tích xung quanh hình trụ Hi vọng các bạn đã có cho mình thông tin hữu ích.