Diện tích toàn phần hình trụ
Diện tích toàn phần hình trụ là tổng diện tích tất cả các mặt bao quanh hình trụ, bao gồm diện tích hai đáy (hình tròn) và diện tích mặt xung quanh (mặt trụ). Nó biểu thị phần diện tích bề mặt cần để bao bọc toàn bộ hình trụ nếu " trải phẳng" ra, và thường được sử dụng trong các bài toán thực tế như tính vật liệu bao phủ, sơn phủ hay thiết kế bề mặt.
Công thức tính diện tích toàn phần hình trụ
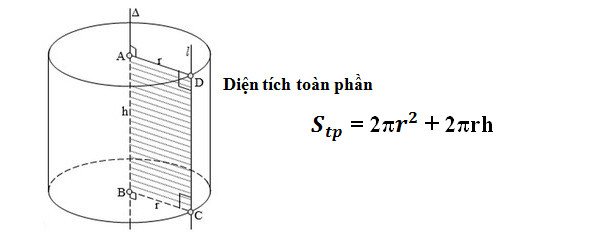
Công thức tính diện tích toàn phần
Giải thích các ký hiệu:
Stp: Diện tích toàn phần của hình trụ
r: Bán kính đáy hình trụ
h: Chiều cao hình trụ
π: Hằng số Pi ≈ 3, 1416
Hiểu bản chất cấu tạo của hình trụ
Hình trụ gồm:
Hai đáy hình tròn → diện tích hai đáy là 2πr²
Một mặt xung quanh (dạng hình chữ nhật khi triển khai) → diện tích là 2πrh
Cách ghi nhớ nhanh
Mẹo 1: Học theo vần
“ Hai đáy tròn trịa – một vòng xung quanh”
→ 2πr² là hai đáy, 2πrh là mặt xung quanh.
Mẹo 2: Gắn với hình ảnh thực tế
Hình trụ giống như lon nước ngọt: có 2 đáy và vỏ bao quanh.
Tưởng tượng mở lon ra: ta có 2 hình tròn (đáy)+1 hình chữ nhật (mặt bên).
Mẹo 3: Viết lại nhiều lần
Ghi công thức Stp=2πr² +2πrh mỗi ngày trong 3-5 phút sẽ giúp nhớ lâu hơn.
Mẹo 4: So sánh với hình tròn
Nếu đã thuộc diện tích hình tròn là πr² , thì công thức hình trụ chỉ cần nhân đôi và thêm phần xung quanh.
 Hình trụ trong không gian
Hình trụ trong không gianKhi nào cần tính diện tích toàn phần?
Khi muốn tính tổng diện tích bề mặt tiếp xúc của hình trụ, như vẽ bao bì, sơn phủ, in tem nhãn…
Khác biệt giữa diện tích xung quanh và diện tích toàn phần là gì?
Diện tích xung quanh: chỉ tính phần bao quanh (mặt bên)
→ Stp=2πrh
Diện tích toàn phần: gồm cả mặt xung quanh và hai đáy
→ Stp=2πr² +2πrh
Nếu chỉ biết chiều cao và chu vi đáy thì tính thế nào?
Ta có thể tìm bán kính r từ chu vi:
Chu vi đáy=2πr ⇒ r=(Chu vi) / (2π)
Sau đó áp dụng công thức như bình thường.
Có cần ghi nhớ cả hai công thức diện tích xung quanh và toàn phần không?
Có. Vì đề bài có thể hỏi riêng từng phần. Việc ghi nhớ giúp áp dụng linh hoạt hơn.
Bài 1:
Một hình trụ có bán kính đáy r=5 cm, chiều cao h=10 cm.
Tính diện tích toàn phần của hình trụ.
Hướng dẫn:
Áp dụng công thức:
S< sub> tp</sub> =2πr² +2πrh
=2π × 5² +2π × 5 × 10
=...
Bài 2:
Một bồn chứa nước hình trụ có đường kính đáy là 1, 2 m và chiều cao 2 m.
Tính diện tích toàn phần cần sơn của bồn chứa.
Gợi ý:
Bán kính r=1, 2 / 2=0, 6 m
Dùng công thức S< sub> tp</sub> =2πr² +2πrh
Bài 3:
Tìm chiều cao h của hình trụ biết bán kính r=4 cm và diện tích toàn phần S< sub> tp</sub> =301.44 cm² .
(Dùng π=3.14)
Gợi ý:
Thay vào công thức và giải phương trình tìm h.
Bài toán vận dụng thực tế
Tình huống 1:
Một công ty muốn in tem lên mặt ngoài lon nước ngọt hình trụ, đường kính đáy 6 cm, cao 12 cm.
Hỏi diện tích mặt ngoài cần in tem là bao nhiêu?
Giải:
Chỉ cần diện tích xung quanh:
S< sub> xq</sub> =2πrh=2π × 3 × 12=226.08 cm²
Tình huống 2:
Bạn muốn dán giấy quanh lon đựng bút hình trụ (không dán đáy và nắp). Lon cao 15 cm, bán kính 4 cm.
Tính diện tích giấy cần dùng.
Giải:
Chỉ tính mặt xung quanh → dùng công thức S< sub> xq</sub> =2πrh
 Học sinh trong giờ toán
Học sinh trong giờ toánTrong hình học không gian, diện tích toàn phần và thể tích là hai đại lượng quan trọng giúp mô tả và tính toán các đặc điểm hình học của hình trụ. Mặc dù chúng thể hiện những khía cạnh khác nhau (bề mặt và dung tích), chúng có mối liên hệ chặt chẽ thông qua các yếu tố hình học cơ bản như bán kính đáy (r) và chiều cao (h).
Nhắc lại công thức cơ bản
Diện tích toàn phần hình trụ:
S< sub> tp</sub> =2πr² +2πrh
(gồm diện tích 2 đáy và mặt xung quanh)
Thể tích hình trụ:
V=πr² h
(thể tích bằng diện tích đáy nhân với chiều cao)
Mối liên hệ gián tiếp qua bán kính và chiều cao
Cả diện tích và thể tích đều phụ thuộc vào bán kính đáy (r) và chiều cao (h). Điều này cho thấy nếu bạn thay đổi r hoặc h, cả diện tích và thể tích đều thay đổi tương ứng.
Ví dụ:
Nếu tăng r, diện tích đáy tăng nhanh hơn mặt xung quanh → cả diện tích và thể tích đều tăng mạnh.
Nếu tăng h, thể tích và diện tích xung quanh đều tăng tỉ lệ thuận.
Từ thể tích suy ra một phần diện tích
Nếu đã biết thể tích V=πr² h và biết r, có thể suy ra h, rồi thế vào công thức S< sub> tp</sub> để tìm diện tích.
Ứng dụng trong thực tế
Trong sản xuất: cần tính cả diện tích để sơn, dán nhãn, và thể tích để chứa chất lỏng hoặc khí.
Trong thiết kế: tối ưu kích thước để tiết kiệm vật liệu mà vẫn đạt dung tích yêu cầu.