Thể tích khối lập phương
Hiểu về hình khối đặc biệt trong không gian ba chiều
Trong hình học không gian, khối lập phương là một trong những hình khối cơ bản và đặc biệt nhất. Nó được tạo thành từ sáu mặt đều là hình vuông, có tám đỉnh và mười hai cạnh bằng nhau. Điều đó có nghĩa là chiều dài, chiều rộng và chiều cao của khối lập phương đều giống nhau. Chính nhờ đặc điểm này mà việc tính thể tích hình phương trở nên dễ dàng hơn rất nhiều so với các hình khối khác như hình trụ, hình hộp chữ nhật hay hình chóp.
Ý nghĩa của thể tích hình hộp lập phương trong toán học và đời sống
Thể tích khối lập phương không chỉ là một khái niệm trong sách giáo khoa, nó còn có tính ứng dụng cao trong thực tế. Việc tính thể tích giúp chúng ta trả lời câu hỏi: “ Khối này chứa được bao nhiêu?” hoặc “ Nó chiếm bao nhiêu không gian?”
Trong các bài toán, thể tích là thước đo lượng “ không gian bên trong” của một vật thể. Còn trong thực tế, bạn có thể áp dụng kiến thức này khi đo đạc, xây dựng, đóng gói sản phẩm, hay tính toán khối lượng vật liệu cần thiết. Biết được cách tính thể tích khối lập phương giúp bạn làm chủ được nhiều tình huống thực tiễn từ lớp học đến công việc hàng ngày.
Khối lập phương cơ bản trong hình học không gianTại sao công thức lại đơn giản đến thế?
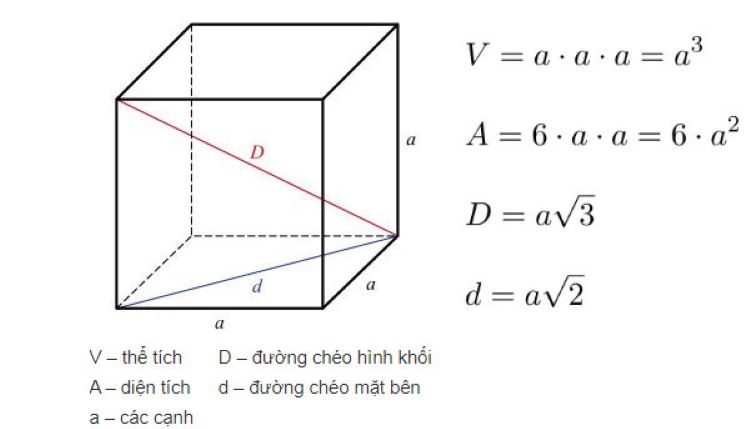
Công thức chuẩn để tính thể tích hình lập phương là:
V=a × a × a
Hoặc viết ngắn gọn hơn là:
V=a³
Trong đó:
V là thể tích hình lập phương
a là độ dài một cạnh của khối
Công thức trên tuy đơn giản nhưng lại cực kỳ mạnh mẽ và hữu ích. Bất cứ khi nào bạn biết chiều dài cạnh, bạn có thể nhanh chóng tính được thể tích mà không cần tới nhiều bước phức tạp.
Minh họa công thức bằng ví dụ thực tế
Giả sử bạn có một chiếc hộp hình lập phương với chiều dài mỗi cạnh là 10cm. Khi đó, thể tích của chiếc hộp sẽ là:
V=10 × 10 × 10=1000 (cm³ )
Điều đó có nghĩa là chiếc hộp có thể chứa tối đa 1000 cm³ không gian bên trong. Ví dụ này không chỉ giúp bạn hình dung rõ hơn về cách tính, mà còn chỉ ra rằng thể tích hình lập phương tăng nhanh theo cấp số mũ khi chiều dài cạnh tăng lên.
Bạn cũng có thể thấy rõ rằng, nếu cạnh của khối lập phương tăng gấp đôi (ví dụ từ 10cm lên 20cm), thì thể tích không chỉ tăng gấp đôi, mà là tăng gấp 8 lần. Điều này xảy ra vì:
20³ =8000 cm³ , trong khi 10³ =1000 cm³

Công thức tính thể tích hình khối lập phương V=a³Thể tích hình lập phương và sự hiện diện trong thực tế
Bạn có bao giờ thắc mắc tại sao trong ngành sản xuất, xây dựng hay thậm chí vận chuyển hàng hóa, người ta lại cần tính toán thể tích? Câu trả lời nằm ở chỗ: thể tích hình lập phương là đơn vị đo giúp xác định rõ lượng không gian cần thiết, nguyên vật liệu sử dụng hoặc dung tích cần thiết của một vật thể.
Hãy tưởng tượng bạn cần xây một khối bê tông hình lập phương có kích thước 1m x 1m x 1m. Khi đó, thể tích hình lập phương này là 1m³ , tương đương với 1000 lít. Dựa vào đó, bạn có thể tính toán lượng xi măng, cát, sỏi và nước cần thiết để tạo nên khối bê tông đó. Nếu không tính chính xác, bạn có thể lãng phí nguyên vật liệu hoặc không đủ để hoàn thành công việc.
Tác động trong giáo dục và kỹ năng tư duy không gian
Trong giáo dục, việc học cách tính thể tích hình lập phương giúp học sinh làm quen với tư duy ba chiều và khả năng hình dung không gian. Đây là một kỹ năng thiết yếu không chỉ cho học sinh theo học ngành kỹ thuật mà còn cho cả những ai làm việc trong thiết kế nội thất, kiến trúc hay lập trình mô phỏng 3D.
Ứng dụng thực tế của thể tích hình lập phươngNhầm lẫn đơn vị đo lường và tác hại không ngờ
Một trong những lỗi phổ biến nhất khi tính thể tích hình lập phương là nhầm lẫn đơn vị đo. Ví dụ, nếu cạnh được cho dưới dạng milimet nhưng bạn tính kết quả ra đơn vị cm³ mà không chuyển đổi, bạn sẽ thu được kết quả sai lệch nghiêm trọng.
Chẳng hạn, nếu một khối lập phương có cạnh là 100mm, và bạn không chuyển về đơn vị cm trước khi tính thể tích, bạn sẽ vô tình tính theo đơn vị sai. Điều đó dẫn đến kết quả sai lệch hàng chục lần. Chính vì vậy, hãy luôn kiểm tra và đồng nhất đơn vị đo trước khi thực hiện bất kỳ phép tính nào.
Nhầm lẫn giữa khối lập phương và hình hộp chữ nhật
Một sai lầm khác thường gặp là áp dụng công thức thể tích hình lập phương cho hình hộp chữ nhật và ngược lại. Khối lập phương yêu cầu ba chiều bằng nhau, còn hình hộp chữ nhật có thể có ba chiều khác nhau. Việc áp dụng công thức V=a³ cho một hình không có các cạnh bằng nhau sẽ cho kết quả sai hoàn toàn.
Không kiểm tra kết quả ước lượng
Trong một số bài toán, việc kiểm tra lại bằng ước lượng giúp bạn xác nhận được rằng kết quả vừa tính ra có hợp lý hay không. Ví dụ, nếu một khối lập phương có cạnh là 2m mà bạn tính ra thể tích là 200m³ thì chắc chắn là sai, vì kết quả đúng phải là 8m³ . Những thao tác kiểm tra đơn giản này giúp bạn tránh mất điểm không đáng trong các bài thi hay bài kiểm tra.
Thể tích hình lập phương không chỉ là một khái niệm cơ bản trong toán học mà còn là công cụ hữu ích trong nhiều lĩnh vực thực tiễn. Việc nắm vững định nghĩa, công thức và cách áp dụng sẽ giúp bạn tự tin hơn trong học tập và công việc.
Hãy luyện tập thêm với các bài toán từ cơ bản đến nâng cao để củng cố kỹ năng và hiểu sâu hơn về mối liên hệ giữa toán học và cuộc sống. Khi đã thành thạo cách tính thể tích khối lập phương, bạn sẽ thấy rằng hình học không gian thực ra không hề khô khan như nhiều người vẫn nghĩ.>> Xem thêm:
Dịch vụ sửa điều hòa tại hà nội