Cách chứng minh 3 điểm thẳng hàng
Khái niệm: Ba điểm thẳng hàng là ba điểm cùng nằm trên một đường thẳng duy nhất. Điều này có nghĩa là nếu ta vẽ một đường thẳng qua ba điểm này, đường thẳng đó sẽ đi qua tất cả các điểm đó mà không bị lệch khỏi chúng.
Mối quan hệ của 3 điểm thẳng hàng:
Ba điểm thẳng hàng là ba điểm khác nhau, cùng nằm trên một đường thẳng. Đây là điều kiện cần để ba điểm đó được gọi là thẳng hàng.
Có một và chỉ một đường thẳng duy nhất đi qua ba điểm bất kỳ. Nếu ba điểm không nằm trên một đường thẳng duy nhất, chúng không phải là ba điểm thẳng hàng.
Quan hệ giữa ba điểm thẳng hàng:
Trong ba điểm thẳng hàng, có một và chỉ một điểm nằm ở giữa 2 điểm còn lại. Điều này có nghĩa là, nếu ta gọi ba điểm là A, B và C, thì một trong ba điểm đó sẽ là điểm nằm giữa hai điểm còn lại.
Lưu ý:
Nếu có một điểm nằm giữa hai điểm còn lại thì ba điểm đó chắc chắn thẳng hàng.
Khi điểm C nằm giữa hai điểm A và B, ta có thể nói rằng:
Hai điểm C và B: Nằm cùng phía với điểm A.
Hai điểm A và C: Nằm cùng phía điểm B.
Hai điểm A và B: Nằm cùng phía đối với điểm C.
Tham khảo: Định lý pytago
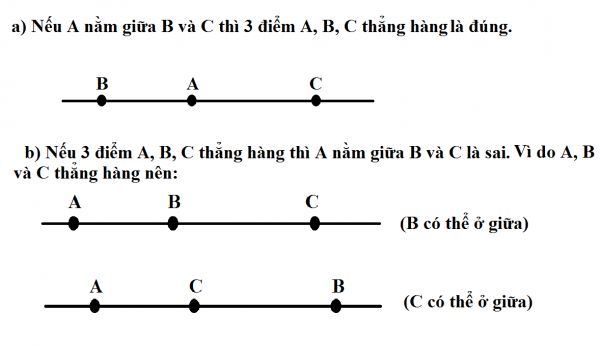
Đặc điểm của 3 điểm thẳng hàng
Ví dụ:
Giả sử, cho ba điểm A, B và C. Nếu điểm C nằm giữa A và B trên một đường thẳng, thì ta có thể kết luận rằng ba điểm A, B, và C là ba điểm thẳng hàng.
Khi chứng minh ba điểm thẳng hàng, có nhiều phương pháp khác nhau để áp dụng tuỳ thuộc vào tình huống và yêu cầu cụ thể. Dưới đây là một số Cách chứng minh 3 điểm thẳng hàng:
- Sử dụng hai góc kề bù: Nếu ba điểm cần chứng minh thuộc vào hai cạnh của một góc kề bù và góc này tạo ra một đường thẳng, ta có thể chứng minh ba điểm này là thẳng hàng.
- Ba điểm thuộc cùng một tia hoặc một đường thẳng bất kỳ: Nếu ba điểm được chỉ ra là nằm trên một tia hoặc một đường thẳng cụ thể, thì chúng chắc chắn là ba điểm thẳng hàng.
- Hai đoạn thẳng song song: Nếu hai đoạn thẳng đi qua hai trong ba điểm và chúng song song với một đường thẳng thứ ba, thì ba điểm này là thẳng hàng.
- Hai đường thẳng vuông góc:Nếu hai đường thẳng đi qua hai trong ba điểm và chúng cùng vuông góc với một đường thẳng thứ ba, ba điểm này cũng là thẳng hàng.
- Đường thẳng đi qua hai điểm cũng đi qua điểm thứ ba: Nếu một đường thẳng đi qua hai điểm trong ba điểm cần chứng minh và nó cũng đi qua điểm thứ ba, ta có thể kết luận ba điểm này là thẳng hàng.
- Áp dụng tính chất đường phân giác của một góc: Nếu ba điểm thỏa mãn tính chất của đường phân giác (chẳng hạn, ba điểm nằm trên đường phân giác của một góc), thì chúng là ba điểm thẳng hàng.
- Áp dụng tính chất của đường trung trực:Ba điểm có thể thẳng hàng nếu chúng thỏa mãn tính chất của đường trung trực của đoạn thẳng (ví dụ, ba điểm này nằm trên một đường trung trực của đoạn thẳng trong tam giác).
- Áp dụng tính chất ba đường cao trong tam giác: Trong một tam giác, ba đường cao của tam giác đồng quy tại một điểm. Nếu ba điểm là ba chân của ba đường cao của một tam giác, chúng là ba điểm thẳng hàng.
- Áp dụng tính chất của hình bình hành: Nếu ba điểm tạo thành một hình bình hành với các tính chất đối xứng, thì ba điểm này sẽ thẳng hàng.
- Áp dụng tính chất của góc nội tiếp đường tròn: Nếu ba điểm nằm trên cùng một đường tròn và thỏa mãn tính chất của góc nội tiếp, thì chúng sẽ thẳng hàng.
- Áp dụng tính chất của góc bằng nhau đối đỉnh: Nếu ba điểm tạo ra các góc đối đỉnh bằng nhau, chúng sẽ thẳng hàng.
- Chứng minh bằng phương pháp phản chứng: Phương pháp phản chứng có thể được áp dụng để chứng minh ba điểm thẳng hàng. Giả sử ba điểm không thẳng hàng, sau đó đi đến một mâu thuẫn để chứng minh rằng ba điểm đó phải thẳng hàng.
- Chứng minh diện tích tam giác của ba điểm bằng 0: Nếu diện tích của tam giác tạo bởi ba điểm bằng 0, tức là ba điểm này nằm trên cùng một đường thẳng.
- Áp dụng tính chất sự đồng quy của các đoạn thẳng: Nếu ba đoạn thẳng đồng quy tại một điểm, thì ba điểm mà các đoạn thẳng này đi qua sẽ thẳng hàng.
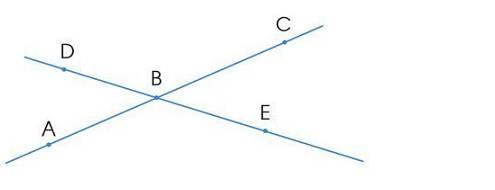
Chứng minh 3 điểm thẳng hàng dựa vào nhiều cách khác nhauDưới đây là một số phương pháp phổ biến và hiệu quả dùng chứng minh 3 điểm thẳng hàng:
Phương pháp 1: Vận dụng tính chất góc bẹt
Cách làm: Chọn một điểm D bất kỳ. Nếu tổng của hai góc ∠ABD + ∠DBC = 180 độ thì ba điểm A, B, C đã cho thẳng hàng.
Giải thích: Ba điểm A, B, C thẳng hàng khi chúng tạo thành một góc bẹt, nghĩa là các điểm này nằm trên cùng một đường thẳng.
Phương pháp 2: Sử dụng tiên đề Ơ-cơ-lít
Cách làm: Cho 3 điểm A, B, C và 1 đường thẳng a. Nếu đoạn thẳng AB song song với a và AC song song với a, ta có thể khẳng định ba điểm A, B, C thẳng hàng.
Giải thích: Đây là một ứng dụng trực tiếp của tiên đề Ơ-cơ-lít trong hình học phẳng, cho phép kết luận ba điểm nằm trên một đường thẳng.
Phương pháp 3: Áp dụng tính chất 2 đường thẳng vuông góc nhau
Cách làm: Nếu đoạn thẳng AB vuông góc với đường thẳng a và đoạn thẳng AC cũng vuông góc với đường thẳng a, thì ba điểm A, B, C thẳng hàng.
Giải thích: Chỉ có một và chỉ một đường thẳng vuông góc với một đường thẳng đã cho đi qua một điểm O, do đó ba điểm A, B, C sẽ nằm trên cùng một đường thẳng.
Hoặc ta cũng có thể áp dụng tính chất đường trung trực để chứng minh ba điểm thẳng hàng, khi ba điểm cùng thuộc một đường trung trực của đoạn thẳng.
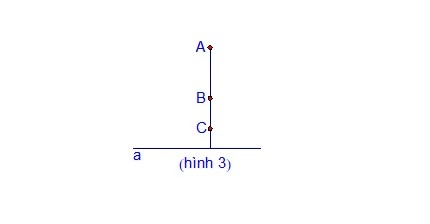
Chứng minh 3 điểm thẳng hàng dựa vào đường vuông góc
Phương pháp 4: Áp dụng tính duy nhất tia phân giác
Cách làm: Nếu hai tia OA và OB là tia phân giác của góc ∠xOy, thì ba điểm O, A, B thẳng hàng.
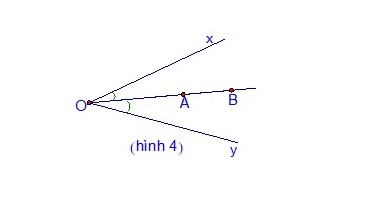
Chứng minh 3 điểm thẳng hàng dựa vào đường phân giác
Giải thích: Mỗi góc chỉ có duy nhất một đường phân giác, vì vậy nếu hai tia là tia phân giác, ba điểm O, A, B sẽ thẳng hàng.
Lưu ý: Ta cũng có thể chứng minh ba điểm thẳng hàng nếu hai tia OA và OB nằm trên cùng một nửa mặt phẳng và ∠xOA = ∠xOB.
Phương pháp 5: Sử dụng tính chất đường trung trực
Cách làm: Giả sử K là trung điểm của đoạn thẳng BD và điểm K’ là giao điểm của đoạn thẳng BD và AC. Nếu điểm K’ cũng là trung điểm của BD và trùng với K, ta có thể kết luận ba điểm A, K, C thẳng hàng.
Giải thích: Mỗi đoạn thẳng có duy nhất một trung điểm, vì vậy khi trung điểm của đoạn thẳng BD trùng với điểm K’ và K, ta có thể khẳng định ba điểm A, K, C thẳng hàng.
Phương pháp 6: Áp dụng tính chất các đường đồng quy
Cách làm: Chứng minh ba điểm thuộc các đường đồng quy trong một tam giác.
Ví dụ: Chứng minh điểm E là trọng tâm của tam giác ABC và đoạn thẳng AM là trung tuyến của góc A, từ đó suy ra ba điểm A, M, H thẳng hàng.
Giải thích: Các đường đồng quy trong tam giác (như 3 đường cao, 3 đường phân giác, hoặc 3 đường trung trực) tạo ra một điểm chung, giúp chứng minh ba điểm thẳng hàng.
Phương pháp 7: Sử dụng phương pháp vectơ
Cách làm: Dùng tính chất của vectơ có cùng phương để chứng minh ba điểm thẳng hàng.
Ví dụ: Chứng minh rằng vectơ AB và vectơ AC có cùng phương, hoặc vectơ CA và vectơ CB, hoặc vectơ AB và vectơ BC có cùng phương thì ba điểm A, B, C sẽ thẳng hàng.
Giải thích: Nếu ba vectơ có cùng phương, thì ba điểm tương ứng với các vectơ này sẽ thẳng hàng.
Tổng Kết:
Các phương pháp chứng minh ba điểm thẳng hàng đều có cơ sở lý thuyết vững chắc và có thể áp dụng trong nhiều trường hợp khác nhau. Việc hiểu và vận dụng đúng phương pháp sẽ giúp giải quyết các bài toán hình học một cách hiệu quả và dễ dàng hơn.
Đề bài: Cho tam giác ABC. Gọi D, E lần lượt là trung điểm của AB, AC. Trên tia đối của tia DC, lấy điểm M thỏa mãn: MD = CD. Trên tia đối của tia EB, lấy điểm N thỏa mãn: EN = BE. Chứng minh A là trung điểm của MN.
Hướng Dẫn Giải
Bước 1: Xét ΔBCD và ΔBMD
Xét tam giác ΔBCD và ΔBMD, ta có các điều kiện sau:
DB=DA (vì D là trung điểm của AB),
∠𝐷1=∠𝐷2 (do đối đỉnh),
DC=DM (theo giả thiết MD=CD).
=> Sử dụng tiêu chuẩn cạnh-góc-cạnh (c-g-c), ta có: ΔBCD≅ΔBMD
Khi đó, ta suy ra được các góc và cạnh sau:
∠𝐶1=∠𝑀(do góc so le trong), BC=AM (cạnh tương ứng trong các tam giác đồng dạng).
Bước 2: Chứng minh BC song song với AM
Từ ∠𝐶1=∠𝑀(góc so le trong), ta có thể suy ra rằng:BC∥AM
Bước 3: Chứng minh BC song song với AN và BC = AN
Tiếp tục áp dụng phương pháp tương tự với tam giác ΔBCE và ΔBNE:
Ta có BC=BE và ∠𝐸1=∠𝐸2 (góc đối đỉnh), BC=AN (do tính chất của tam giác ΔBCE và ΔBNE).
=> Từ đó, ta có BC∥AN và BC=AN.
Bước 4: Kết luận ba điểm A, M, N thẳng hàng
Từ các điều kiện đã chứng minh, ta có:
BC∥AM và BC∥AN,AM=AN.
=> Như vậy, A,M,N thẳng hàng vì BC∥AM∥AN và AM=AN.
Tóm Tắt Kết Quả
Chứng minh rằng ba điểm A, M, N thẳng hàng, và sau đó chứng minh rằng
AM=AN. Từ đó, suy ra A là trung điểm của MN.
Nhận Xét
Trong quá trình chứng minh, việc chứng minh ba điểm A, M, N thẳng hàng trước và sau đó chứng minh
𝐴𝑀=𝐴𝑁là một bước quan trọng giúp kết luận A là trung điểm của MN.