Bảy hằng đẳng thức đáng nhớ
Hằng đẳng thức là một đẳng thức mà luôn đúng với mọi giá trị của các đại lượng trong biểu thức. Nói cách khác, đó là các mối quan hệ toán học đúng với mọi giá trị của các biến số mà không có ngoại lệ. Hằng đẳng thức thể hiện một mối quan hệ bất biến giữa các đại lượng trong mọi trường hợp.
Ví dụ về một hằng đẳng thức:(a+b)2 = a2 +2ab +b2 là một hằng đẳng thức vì:
- Nhị thức bên trái (a+b)2 và nhị thức bên phải a2 +2ab +b2 được nối với nhau bởi dấu =
- Đẳng thức này luôn đúng với mọi giá trị của a, b
Các đặc điểm của hằng đẳng thức:
- Đúng với mọi giá trị của biến: Hằng đẳng thức luôn đúng không phụ thuộc vào giá trị cụ thể của các đại lượng trong đó.
- Dễ nhận diện trong các bài toán: Hằng đẳng thức là công cụ mạnh mẽ giúp giải quyết các bài toán biến đổi, rút gọn biểu thức hoặc chứng minh đẳng thức.
- Là cơ sở của nhiều phương pháp giải toán: Các hằng đẳng thức như hằng đẳng thức đáng nhớ trong đại số được áp dụng rất nhiều trong việc giải các phương trình và bất phương trình.

7 hằng đẳng thứcBảy hằng đẳng thức đáng nhớ là những công thức toán học cơ bản nhưng vô cùng quan trọng, đặc biệt trong việc biến đổi các biểu thức đại số.
Dưới đây là 7 hằng đẳng thức đáng nhớ:
1. Bình phương của một tổng: (A + B)² = A² + 2AB + B²
Phát biểu bằng lời: Bình phương của một tổng bình phương của số đầu tiên cộng với hai lần tích của hai số đó, rồi cộng thêm bình phương của số thứ hai.
Ví dụ:
a) x2 + 2x + 1 = (x)²+ 2.(x).(1) + (1)² = (x + 1)²
b) 9x² + y² + 6xy = 9x² + 6xy + y² = (3x)² + 2.(3x).(y) + (y)² = (3x + y)²
2. Bình phương của một hiệu: (A - B)² = A² - 2AB + B²
Giải thích: Bình phương của một hiệu bằng lấy bình phương của số đầu tiên, trừ đi hai lần tích của số đầu tiên với số thứ hai, rồi cộng thêm bình phương của số thứ hai.
c) 25a² + 4b² – 20ab = 25a² – 20ab + 4b² = (5a)² – 2.(5a).(2b) + (2b)² = (5a + 2b)²
3. Hiệu hai bình phương: A² - B² = (A + B)(A - B)
Phát biểu bằng lời: Hiệu của bình phương hai số bằng tích của tổng hai số đó và hiệu hai số đó.
4. Lập phương của một tổng: (A + B)³ = A³ + 3A²B + 3AB² + B³
Phát biểu bằng lời: Khi lập phương của tổng hai số, ta sẽ có lập phương của số đầu tiên cộng với ba lần tích bình phương của số đầu tiên nhân với số thứ hai, cộng với ba lần tích của số đầu tiên nhân với bình phương của số thứ hai, rồi cộng thêm lập phương của số thứ hai.
Tham khảo: Cách chứng minh 3 điểm thẳng hàng
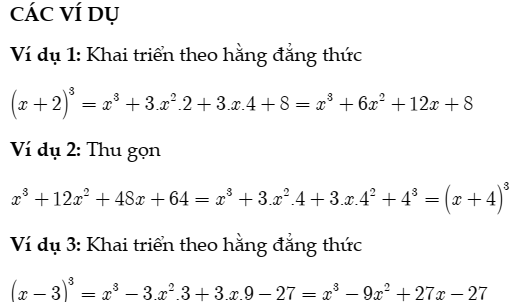
Ví dụ về hằng đẳng thức bậc 3
5. Lập phương của một hiệu: (A - B)³ = A³ - 3A²B + 3AB² - B³
Phát biểu bằng lời: Khi lập phương của hiệu hai số, ta sẽ có lập phương của số đầu tiên, trừ đi ba lần tích bình phương của số đầu tiên nhân với số thứ hai, cộng với ba lần tích của số đầu tiên nhân với bình phương của số thứ hai, rồi trừ đi lập phương của số thứ hai.
Ví dụ: (2x – 3y)³ = (2x)³ – 3.(2x)² (3y) + 3(2x).(3y)² – (3y)³ = 8x³ – 36x2y + 54xy² – 27y³
6. Tổng hai lập phương: A³ + B³ = (A + B)(A² - AB + B²)
Phát biểu bằng lời: Tổng của hai lập phương bằng tích của tổng hai số đó với bình phương thiếu của hiệu hai số đó.
7. Hiệu hai lập phương: A³ - B³ = (A - B)(A² + AB + B²)
Phát biểu bằng lời: Hiệu của hai lập phương bằng tích của hiệu hai số đó với bình phương thiếu của tổng hai số đó.
Bảy hằng đẳng thức đáng nhớ là các công thức đại số cơ bản và quan trọng mà học sinh, sinh viên cần nhớ và áp dụng trong việc giải các bài toán đại số. Các hằng đẳng thức này giúp việc xử lý các biểu thức toán học trở nên nhanh chóng và chính xác hơn. Chúng có ứng dụng trong nhiều tình huống toán học, từ việc rút gọn biểu thức, nhân phá đa thức, giải phương trình, cho đến phân tích đa thức thành nhân tử. Dưới đây là lý do tại sao chúng gọi là "Bảy hằng đẳng thức đáng nhớ":
Rút gọn biểu thức:
Các hằng đẳng thức giúp ta biến các biểu thức phức tạp thành những dạng đơn giản hơn, dễ dàng tính toán và nhận ra các mối quan hệ. Việc áp dụng các hằng đẳng thức giúp ta dễ dàng rút gọn và tối ưu hóa bài toán.
Nhân phá đa thức:
Khi gặp các đa thức có dạng đặc biệt, các hằng đẳng thức giúp chúng ta tính nhanh các tích mà không cần thực hiện phép nhân từng phần. Các dạng đặc biệt như bình phương của tổng hoặc hiệu, hiệu của hai bình phương, v.v., đều có công thức riêng giúp tính toán nhanh.
Giải phương trình:
Khi giải phương trình đại số, chúng ta thường xuyên gặp các bài toán mà áp dụng các hằng đẳng thức để biến phương trình về dạng tích. Điều này giúp dễ dàng tìm được nghiệm của phương trình bằng cách giải các tích.
Phân tích đa thức thành nhân tử:
Các hằng đẳng thức giúp phân tích các đa thức phức tạp thành tích của các đa thức đơn giản hơn. Việc phân tích này thường rất hữu ích khi giải phương trình bậc cao hoặc khi cần biểu diễn lại một đa thức dưới dạng dễ thao tác hơn.
Dưới đây là 5 cách học thuộc các hằng đẳng thức dễ dàng:
Hiểu rõ bản chất của hằng đẳng thức
Trước khi học thuộc, hãy hiểu rõ ý nghĩa và ứng dụng của từng hằng đẳng thức. Cố gắng tưởng tượng mỗi hằng đẳng thức như một công thức toán học mô tả một quy tắc, một quy luật chặt chẽ mà bạn có thể thấy trong cuộc sống hoặc các bài toán. Khi bạn hiểu sâu về bản chất, việc ghi nhớ sẽ dễ dàng hơn nhiều.
Ví dụ:
(a + b)² = a² + 2ab + b²: Điều này nói rằng khi bạn bình phương tổng của hai số, bạn sẽ nhận được bình phương của số đầu tiên, cộng với hai lần tích của số đầu tiên và số thứ hai, cộng với bình phương của số thứ hai.

Một số mẹo học thuộc hằng đẳng thức đáng nhớ
Sử dụng phương pháp chia nhỏ và học từng phần
Thay vì học thuộc toàn bộ hằng đẳng thức một lúc, bạn hãy chia nhỏ từng phần của hằng đẳng thức và học dần dần. Ví dụ, khi học công thức (a + b)², bạn có thể học "bình phương của a" trước, sau đó học "bình phương của b", và cuối cùng là "hai lần tích của a và b". Khi ghép lại tất cả, bạn sẽ nhớ dễ dàng hơn.
Áp dụng vào bài tập thực tế
Cách tốt nhất để ghi nhớ các hằng đẳng thức là áp dụng chúng vào các bài tập thực tế. Thực hành là phương pháp hiệu quả nhất để củng cố kiến thức. Khi bạn áp dụng hằng đẳng thức vào các bài tập, bạn sẽ hiểu được công thức đó có ý nghĩa như thế nào và nhớ lâu hơn.
Ví dụ:
Giải bài tập với các hằng đẳng thức (a + b)² trong các bài toán mở rộng hoặc chuyển các biểu thức phức tạp về dạng đơn giản hơn.
Sử dụng hình ảnh hoặc ví dụ minh họa
Đôi khi, một hình ảnh hoặc ví dụ cụ thể sẽ giúp bạn hình dung và ghi nhớ hằng đẳng thức dễ dàng hơn. Ví dụ, khi học (a + b)², bạn có thể vẽ một hình vuông với cạnh là (a + b), sau đó chia nó thành các phần để thấy rõ cách thức phát sinh công thức. Việc hình dung bằng hình vẽ giúp tạo mối liên hệ trực quan, giúp bạn nhớ lâu hơn.
Lặp lại và ôn tập thường xuyên
Để ghi nhớ lâu dài, bạn cần lặp lại và ôn tập thường xuyên. Hãy dành ít nhất 5-10 phút mỗi ngày để ôn lại các hằng đẳng thức. Bạn có thể sử dụng phương pháp ghi chép hoặc viết lại công thức để khắc sâu vào bộ nhớ. Ngoài ra, việc kiểm tra lại các hằng đẳng thức trong các bài tập cũng giúp bạn ôn lại chúng hiệu quả.
Một cách thú vị là bạn có thể áp dụng kỹ thuật Flashcards (thẻ học) để tạo ra các câu hỏi và trả lời về các hằng đẳng thức, kiểm tra lại khi bạn có thời gian rảnh.
Bằng cách áp dụng những phương pháp trên, việc học thuộc và sử dụng các hằng đẳng thức sẽ trở nên dễ dàng hơn và bạn sẽ cảm thấy tự tin hơn khi giải các bài toán toán học. Chúc bạn áp dụng thành công!